
Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional
https://dx.doi.org/10.19137/praxiseducativa-2023-270114

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional
ARTÍCULOS
Continuidades y discontinuidades en las Trayectorias Escolares: una mirada desde la transición primaria-secundaria a partir de la evaluación de los aprendizajes en el área de Matemática.
Continuities and discontinuities in School Trajectories: a look from the primary-secondary transition from the Mathematics assessment
Continuidades e descontinuidades nas Trajetórias Escolares: um olhar da transição primário-secundário a partir da avaliação da aprendizagem na área da Matemática
Carolina Scavino
Universidad Nacional de General Sarmiento, Argentina
cscavino@campus.ungs
ORCID 0000-0003-3840-8469
Resumen: El artículo se enmarca en un estudio de casos múltiples, realizado en la región educativa IX de la Provincia de Buenos Aires-Argentina, orientado al análisis de las continuidades y discontinuidades de las trayectorias escolares en las transiciones primaria/secundaria y secundaria/superior, a partir del análisis de la evaluación de los aprendizajes. Este trabajo, presenta los resultados obtenidos sobre el estudio de uno de los casos, sobre las formas de evaluar los aprendizajes en el área de matemática entre el último año del primario y el primer año del secundario. Se tuvieron en cuenta, el punto de vista de los docentes, las percepciones de estudiantes y el análisis comparado de documentos normativos escolares (diseño curricular y régimen académico de cada nivel). El trabajo permite ilustrar las múltiples dimensiones en juego en el pasaje de un nivel a otro y sugiere algunos temas para mejorar las condiciones que garanticen trayectorias escolares continuas.
Palabras claves: Transición escolar; Evaluación de aprendizajes; Matemática; Trayectorias escolares; Primaria-secundaria.
Abstract: The article is framed in a study of multiple cases, carried out in the educational region IX of the Province of Buenos Aires-Argentina, oriented to the analysis of the continuities and discontinuities of the school trajectories in the primary/secondary and secondary/superior transitions, from the analysis of the assessment. This work presents the results obtained from the study of one of the cases, on the ways of mathematics assessment between the last year of primary school and the first year of secondary school. The point of view of the teachers, the perceptions of students and the comparative analysis of school normative documents (curricular design and academic regime of each level) were taken into account. The work allows to illustrate the multiple dimensions at stake in the passage from one level to another and suggests some topics to improve the conditions that guarantee continuous school trajectories.
Keywords: School transition; Assessment; Mathematics; School trajectories; Primary-secondary
Resumo: O artigo está enquadrado em um estudo de casos múltiplos, realizado na região educacional IX da Província de Buenos Aires-Argentina, orientado para a análise das continuidades e descontinuidades das trajetórias escolares nas transições primária/secundária e secundária/superior, a partir da análise da avaliação da aprendizagem. Este trabalho apresenta os resultados obtidos a partir do estudo de um dos casos, sobre as formas de avaliação da aprendizagem na área da matemática entre o último ano do ensino básico e o primeiro ano do ensino secundário. Foram levados em conta o ponto de vista dos professores, as percepções dos alunos e a análise comparativa de documentos normativos escolares (desenho curricular e regime acadêmico de cada nível). O trabalho permite ilustrar as múltiplas dimensões em jogo na passagem de um nível para outro e sugere alguns tópicos para melhorar as condições que garantem trajetórias escolares contínuas.
Palavra-Chave: Transição escolar; Avaliação da aprendizagem; Matemática; Trajetórias escolares; Primário-secundário
Recibido: 2022-07- 23 | Revisado: 2022-10-27 | Aceptado: 2022-11-27
Introducción
“En general nuestro modo de abordaje psicoeducativo está más atento a las competencias de base de los sujetos, por ejemplo cuando un sujeto no aprende la matemática de tercero sospechamos de su competencia cognitiva y no de su probable pobre historia de aprendizaje de la matemática de segundo y la matemática de primero. Esta confusión se produce al dicotomizar la competencia intelectual de las historias concretas de los aprendizaje de los sujetos”
(Baquero, 2014)
El trabajo se inscribe en un proyecto de investigación desarrollado entre 2016-2019[1], que actualmente continúa en el proyecto UNGS-IDH (2020-2022)[2], que se propuso analizar las trayectorias escolares a partir del estudio de las transiciones escolares primaria/secundaria y secundaria/superior.
Sostiene, como hipótesis, que algunos problemas para lograr tránsitos sostenidos, continuos, completos y con aprendizajes relevantes por el sistema escolar podría relacionarse con la heterogeneidad y discontinuidad de criterios y modalidades de evaluación sumativa en los distintos niveles educativos.
Para abordar este tema, se realizó un estudio de casos múltiples, centrado en el análisis de las transiciones escolares, a través de la reconstrucción de trayectos plausibles[3] que podría realizar un/a estudiante. Se propuso un abordaje novedoso al centrar la mirada en el estudio de la evaluación de aprendizaje de cuatro áreas curriculares (Matemática, Prácticas del Lenguaje, Ciencias Sociales y Ciencias Naturales) prioritarias en la formación del estudiantado.
Su objeto de estudio se centró en la evaluación de aprendizajes teniendo en cuenta: los instrumentos de evaluación sumativa, los criterios docentes respecto a qué y cómo evaluar y los contenidos mínimos requeridos o esperados en cada nivel escolar para el avance en los aprendizajes de los/as estudiantes (Perrenoud, 2015; Camillioni, 2004; Camillioni et al., 1998; Ravela, 2009; Ravela et al., 2009; Martinez-Rizo, 2015; Elola, Zanelli y Toranzos, 2010). A su vez, como marco conceptual, se reconoce que el cambio de un nivel educativo a otro implica, para los/as estudiantes, una reorganización y adaptación a nuevas reglas de comportamiento (Baquero et al., 2009; Terigi, 2014) así como a nuevas condiciones pedagógico-didácticas y de trabajo académico, en torno a los campos de saber (Feldman y Palamidesi, 2015; Feldman et al., 2017; Amantea et al., 2019; Sadovsky y Lerner, 2006).
En este artículo, se analizan las continuidades y discontinuidades sobre los criterios de evaluación y acreditación, en el área de Matemática, de cada nivel escolar y su posible compromiso, para lograr un pasaje sostenido de los/as estudiantes en la transición escolar . Por “continuidad”, se entiende el sostenimiento de condiciones pedagógico-didácticas que den lugar a que los nuevos aprendizajes puedan resignificar adquisiciones previas, integrándose en campos conceptuales más abarcativos y por “discontinuidad”, se entiende la falta de integración de dichas condiciones (Terigi, 2015).
Metodología
Los resultados que se presentan a continuación surgen de un estudio de casos múltiples (Stake, 2005), realizado entre 2016 y 2019, en instituciones de niveles primario, secundario y superior, relacionadas entre sí a partir de la reconstrucción de recorridos escolares posibles (trayectos plausibles) de estudiantes ingresantes al Curso de Aprestamiento Universitario (CAU)[4] de la Universidad Nacional General Sarmiento (UNGS).
Para determinar los casos y recorridos posibles, se desarrolló un proceso de selección en dos etapas: primero, se identificaron las escuelas secundarias de procedencia de los/as ingresantes a la UNGS[5] y, luego, se seleccionaron escuelas de gestión estatal que proveían, de manera estable, un mínimo de 25 ingresantes a dicha unidad académica, en el período analizado. Se seleccionaron seis escuelas para desarrollar el trabajo de campo.
La segunda etapa consistió en identificar las escuelas primarias de mayor procedencia en las escuelas secundarias participantes. La muestra intencional[6] quedó conformada por los siguientes casos:
Tabla 1
Configuración de la Muestra Intencional
|
Casos |
Escuela Primaria 6to año |
Escuela Secundaria 1er y 6to año (o 7mo año) |
UNGS CAU |
|
1 |
A |
A |
CAU |
|
2 |
B |
B |
|
|
3 |
C |
C |
|
|
4 |
D |
D (Técnica) |
|
|
5 |
Sin identificación de escuela primaria |
E (Técnica) |
|
|
|
Sin identificación de escuela primaria |
F |
Eso representa un recorrido institucional plausible para estudiantes hipotéticos. La unidad de observación la constituyeron los/as docentes, estudiantes y un evento evaluativo[7] de cada uno de los años escolares implicados en la muestra; y la unidad de análisis, fue la perspectiva de docentes y estudiantes respecto a criterios y prácticas de evaluación de aprendizaje de cuatro áreas curriculares (Matemática, Práctica del Lenguaje, Ciencias Sociales y Ciencias Naturales).
Las técnicas para la recolección de datos fueron: relevamiento documental[8]; entrevistas a docentes y estudiantes por años y áreas curriculares; recolección de instrumentos de evaluación sumativa; observación de un evento evaluativo; y la administración de un cuestionario autoadministrado o grupo focal[9].
En este trabajo, se presenta el análisis de las continuidades y discontinuidades, vinculado al área de Matemática, en la transición primaria-secundaria en uno de los casos estudiados. Por un lado, se comparan orientaciones y prescripciones[10] de los diseños curriculares (en adelante, DC) para 6to año de primaria y 1er año de secundaria para el área de Matemática y los criterios de acreditación, promoción y aprobación, vigente en el Régimen Académico de cada nivel escolar y, por otro, se analizan los criterios de evaluación (qué y cómo se evalúa) y acreditación (qué contenidos son necesarios para aprobar y cuáles requeridos para avanzar) que sostienen las/os docentes entrevistados/as en el caso de estudio. También se presenta un análisis de un evento evaluativo[11] y las percepciones de los estudiantes[12] sobre la evaluación de los aprendizajes.
Este análisis dio lugar a la escritura de un relato descriptivo, para un trayecto plausible, de un/a estudiante hipotético/a, a partir de la reconstrucción del recorrido escolar identificado en la selección de las instituciones, expuesto al inicio de la metodología.
Si bien los datos del trayecto plausible no son posibles de generalizarse, las afirmaciones expuestas tienen valor por lo que describen y permiten advertir sobre posibles discontinuidades en las trayectorias escolares al momento de la transición escolar.
La Transición de 6to año de Nivel Primario a 1er año Nivel Secundario desde el Área Matemática
Caracterización de las continuidades y discontinuidades desde los Diseños Curriculares y el Régimen Académico
Un primer análisis fue identificar el modelo organizativo del currículum y los contenidos a ser evaluados. El espacio curricular Matemática[13], siguiendo los criterios de Davini (1999), conserva, a lo largo de los diferentes niveles escolares, un criterio disciplinar que no sufre modificaciones en su denominación y establece, para cada nivel, objetivos claros para la promoción de los aprendizajes. Sin embargo, si se analiza el equilibrio entre los contenidos a enseñar, la recuperación de las experiencias previas de los/as alumnos/as y las finalidades de cada nivel, se pueden realizar algunas observaciones.
Desde el punto de vista de la estructura curricular, los saberes matemáticos se diferencian, claramente entre sí, por una progresiva complejidad en el avance entre niveles. Sin embargo, no se identifica una integración que oriente el trabajo docente de cara a la transición. Si bien existen documentos complementarios orientados a la transición (Briscioli y Rio, 2018), estos documentos no dialogan o se integran a las orientaciones que brinda el DC sobre la enseñanza de la Matemática, dejando a criterio del/la docente esta tarea de integración/articulación[14].
Desde el punto de vista de la unidad pedagógica, Matemática, a lo largo de la transición primaria/secundaria, es definida como una asignatura o materia manteniendo un criterio disciplinar de los contenidos. Lo cual representa un enfoque conceptual y metodológico claramente delimitado.
Finalmente, desde el punto de vista de las expectativas de logro del estudiantado u objetivos de aprendizaje y las orientaciones para la evaluación[15], el último año del nivel primario define las expectativas en función del ciclo, sin orientaciones particulares respecto a la evaluación que se debe desarrollar en cada año. Son las instituciones de nivel primario las que deben realizar un trabajo de integración y articulación entre los años escolares, así como una definición conjunta sobre qué y cómo evaluar. Mientras, el DC para el primer año del secundario establece objetivos de logros particulares para ese año escolar y brinda orientaciones para la evaluación: propone evaluar el proceso, comunicando con claridad a los/as estudiantes lo que se espera de ellos/as y enfatiza que la evaluación debe evitar la memorización, advirtiendo que los instrumentos no evalúen solo mecanismos.
A partir de lo descripto, Matemática mantiene una continuidad pedagógica como espacio curricular y se identifica, en ambos casos, una problemática común en torno a la enseñanza de la matemática ⎯evitar que la matemática sea reducida a la resolución mecánica y memorística de las operaciones⎯[16]; sin embargo, es posible que la definición de las expectativas de logro por ciclo o año y la falta de incorporación de la temática de la transición al diseño curricular, de modo integrado, genere condiciones de discontinuidad, ya que deja a criterio de las instituciones educativas y sus posibilidades de articulación entre otras instituciones los acuerdos y delimitación de criterios comunes.
Un segundo análisis sobre la continuidad y discontinuidad en la transición primaria-secundaria estuvo en relación con los criterios de calificación, promoción y acreditación[17] que sostienen los Regímenes Académicos en cada uno de los niveles educativos estudiados.
En el nivel primario, se establece que el equipo de conducción, en consenso con el equipo docente, elabore un proyecto institucional de evaluación expresando criterios y estrategias por área. A su vez, establece que la evaluación será integral, con análisis de los avances del/la estudiante. El segundo ciclo, organizado por trimestres, calificará con una escala de 4 a 10, aprobándose con 7, y cada trimestre deberán garantizar diferentes modos de evaluación (escrita, oral, trabajos prácticos individuales o grupales, armado de glosario, etc.). El/la docente hará tres informes de evaluación con calificación y un cuarto informe final.
En el nivel secundario, el Régimen Académico no establece el tipo de evaluación que se promueve. Cada trimestre tendrá una calificación constituida por, al menos, tres calificaciones parciales, siendo una de ellas obtenida por una evaluación escrita. Dicha calificación final surgirá del promedio de las tres o más calificaciones parciales en una escala del 1 al 10. La calificación final será una nota promedio anual, de las notas trimestrales, en la escala de 1 a 10, aprobando con 7 puntos o más y habiendo tenido, en el último trimestre, una nota mínima de 4 puntos. Si el/la estudiante no aprobó el último trimestre, deberá asistir a una semana de apoyo y orientación. A su vez, si en la materia se implementase una evaluación integradora, esta se calificará en la escala del 1 al 10, aprobándose con 7 puntos, y formará parte del promedio de la calificación final de la asignatura[18].
A partir de lo expuesto, se observa que tanto para el nivel primario como para el secundario la acreditación es anual y se organiza trimestralmente, pudiendo variar los tipos de evaluación que se contemplan. Cada nivel educativo tiene diferentes grados de precisión respecto al tipo de evaluación que se realiza: la acreditación trimestral debe contemplar diferentes modalidades de evaluación (nivel primario) o tres calificaciones numéricas parciales, siendo una de ellas de una evaluación escrita (nivel secundario). Así, aunque hay acuerdos en que la acreditación debe realizarse teniendo en cuenta diversidad de evaluaciones, se observa un peso diferencial entre niveles educativos respecto a las calificaciones. La relación evaluar-calificar, según se expresa en la normativa, pareciera tener mayor adherencia en el nivel secundario que en el primario, en tanto, en la secundaria, cuando se evalúa, se califica y, para la primaria, las evaluaciones son insumos para que el/la docente analice el proceso y lo exprese en una calificación. En este sentido, podría plantearse una discontinuidad entre niveles respecto a la relación evaluación y calificación.
Caracterización de las continuidades y discontinuidades a partir de formas de evaluar Matemática en actividades escolares situadas
El fin de la escuela primaria
Juan es estudiante de una escuela primaria de jornada simple de gestión estatal, ubicada en una zona céntrica del conurbano bonaerense. La escuela constituye una unidad académica de prestigio en la zona, en la cual funciona también una escuela secundaria y un Instituto Superior de Formación Docente.
Al terminar la primaria, Juan sabía que continuaría sus estudios en dicha escuela. La secundaria recibe el 50 % de su matrícula de su escuela primaria. Varios/as de sus compañeros/as pensaban como él, que la secundaria sería “medio difícil”. Que ahí un 8 sería como un 10 y que “necesitas más de 9 para no llevarte la materia”. También pensaba que “si repetís por segunda vez te echan de la escuela; y también si faltas y no las justificas”. Pensaba que las pruebas serían “más desafiantes (pero) tampoco gran cosa. Depende de cuánto estudias. ¡Ahí sí! Muchas veces tenés pruebas sorpresa. Por eso todos los días hay que repasar lo que viste el día anterior”. (Voces de estudiantes de 6to año de primera del caso 1(en adelante Voces 6to EP C1), grupo focal, 11 de Octubre de 2017)
Los dichos de Juan muestran que, él como sus compañeros/as de curso, “no se sienten preparados para entrar en la secundaria”. Se sienten “muy chiquitos todavía” y les falta seguridad. La secundaria la viven con el desconocimiento de lo que supone un cambio y, si bien pueden anticipar o imaginar lo que vendrá, no lo han vivido[19], pero saben que cuentan con su historia como estudiantes para afrontar lo que se viene: “en la primaria hacen lo que hacen siempre, levantarse temprano el día de la prueba para repasar”, “estudiar de noche” o contar a mamá lo que se acuerdan o bien esta les hace preguntas. También saben que “estudiar de memoria es un riesgo, te pones nervioso y te olvidas”, entonces hay que practicar con tus propias palabras frente a un espejo. En el caso particular de Matemática, algunos consideraban que “a veces no es necesario estudiar sino tan solo practicar o repasar” y las tablas cuestan, por eso “hay que estudiarlas”, como alguna vez le aconsejaron en la escuela. (Voces 6to EP C1, grupo focal, 11 de Octubre de 2017)
Al término de la primaria, los/as alumnos/as tienen una idea general sobre el estudio y sobre cómo estudiar Matemática, en particular. Para ellos/as, Matemática es “practicar o repasar”. Esta idea del campo disciplinar se ha forjado en sus años de escolarización primaria. Vinculan la Matemática a un “saber hacer”, con un dominio procedimental del objeto matemático, y el “estudio” implica “repasar o recordar”.
En 6to de primaria en el área de matemática, Juan tuvo una docente nueva. Había ingresado a la escuela ese año. Era una mujer experimentada, con 20 años de antigüedad en la docencia, pero que debía adecuarse a las formas de trabajo de la nueva institución. Ella era organizada. Llevaba una agenda diaria donde anotaba todas las actividades que daba al grupo, y tenía una planilla para el seguimiento de los/as alumnos/as: “voy anotando (…) numeración, escritura. Trabajo en clase, trabajo práctico, fecha… todo. Esto, es todo el proceso que el chico va haciendo” (Docente 6to año primaria matemática del caso 1 (en adelante D 6to EP Mate C1), entrevista, 14 de junio del 2017). Estos registros los realizaba por iniciativa personal, es decir, a Juan le tocó “en suerte” esta docente, pero le podría haber tocado otra/o con años en la escuela y con otra modalidad de trabajo, porque las instituciones no suelen regular estos aspectos.
Para el curso de Juan, la docente organizó su enseñanza de la matemática según la propuesta del manual de Ed. Ediba porque “es conciso y preciso. Tenía los contenidos y el grado iba a responder de acuerdo a las actividades” (D 6to EP Mate C1, entrevista, 14 de junio de 2017).
Transcurrido el primer trimestre, notó que el curso tenía algunas dificultades en el dominio del conocimiento matemático y, según su “lectura”[20], fue a causa de que, en años anteriores, no se dictaron algunos contenidos o no hubo un criterio común respecto a la enseñanza de la matemática:
Te encontrás con que un estudiante hace una cosa y el otro dice “no, no sé”. En cuarto (la) división es cómo se descompone, la de quinto resta sucesiva y llegas vos a sexto y decís “¿Qué hago?”, prefiero que sea la mecánica y el chico dice: “no lo sé hacer”. (…) Toda escuela tiene que tener un criterio. (...) Pero para lograr eso, tengo que trabajar en equipo. El docente de primero se tiene que reunir con el de segundo, “Hasta acá llegué”. Vos vas a tener tercero. ¿Qué viste? ¿Arranco de acá? ¿No repito el mismo cuento? Si no es una repitencia. Repito, repito, repito y el chico pierde el tiempo. (D 6to EP Mate C1, entrevista, 14 de junio de 2017)
A partir de lo señalado por la docente, se comprende que el dominio del campo matemático con el que egresa un/a alumno/a también tiene una dimensión institucional, en la que, por defecto, “repetir contenidos de años anteriores” sería la estrategia docente frente a la desarticulación o falta de un criterio institucional común.
Si bien se sabe, desde el punto de vista didáctico (Parra y Saiz, 1997), que un/a estudiante puede tener diferentes formas de abordar/resolver las operaciones aritméticas, a partir del señalamiento docente, queda la duda sobre cómo se retoma eso en la enseñanza. La reiteración de contenidos, “repito, repito y el chico pierde el tiempo”, no indica una concepción constructiva del proceso que implica para los/as estudiantes el dominio matemático, por el contrario, denuncia el problema de enseñar en grandes redes institucionales en grupos heterogéneos (Terigi, 2010). La “repetición” sería un indicio de una falta de articulación institucional: no identifico lo que traen los/as estudiantes y no sé qué ni cómo lo vieron.
Sobre la evaluación, la docente comenta (D 6to EP Mate C1, entrevista, 14 de junio de 2017): “(evalúo) todo en base a lo que trabajamos (…) les digo ‘bueno, vamos a tener prueba, vamos a hacer un repaso, ¿Qué vimos?’ y hacemos todos ejercicios”. Su objetivo es “ver si adquirieron todos esos conocimientos que estuviste trabajando durante el mes o el trimestre” y, considerando que muchos estudiantes viven la prueba con tensión: “siempre me enfoco más en un trabajo práctico en clase con nota”. Sin embargo, esta no es la única vía para evaluar. También tiene en cuenta si los/as estudiantes pasan al pizarrón, les da un ejercicio y evalúa si lo pueden resolver o si, al terminar, están ayudando a los/as demás. Para la docente, esto es un indicador de que sus estudiantes: “están preparados para estar en la secundaria, lo pudo resolver solo y sin ayuda”.
Otro aspecto importante que tiene en cuenta al momento de evaluar es cómo resuelven las situaciones problemáticas:
Hay cinco pasos que tenés que saber: tenés que comprender el enunciado del problema, tenés que saber los datos que vos tenés, qué podes hacer con esos datos y cuál es la pregunta que tenés que resolver (…), ellos te dicen “seño, ¿suma o resta?”, pero tenés que saber todos esos pasos para resolver un problema, no es suma o resta. Entonces eso lo evalúo. (D 6to EP Mate C1, entrevista, 14 de junio de 2017)
Y lo hace a través de un trabajo práctico donde solicita, por ejemplo, “armar cinco preguntas que se resuelvan con la división y la multiplicación” (D 6to EP Mate C1, entrevista, 14 de junio de 2017)
Las pruebas escritas son individuales y espera que, además de que “la puedan resolver”, la lean. Para ello, de vez en cuando, pone alguna trampa o un resultado cambiado en la consigna:
El (estudiante) despierto lo saca rápido. El que no, no lo saca. Tienen que estudiar. (…) más que nada es para ver la concentración y si está leyendo la prueba. Porque he visto “¿Cuál es el resultado?” y lo ponen. El que detecta sabe que hay un error en la primera leída que hizo de la prueba. Si no detecta, es porque no leyó nada directamente. Más que nada busco eso. Que lean la prueba. (D 6to EP Mate C1, entrevista, 14 de junio de 2017)
Para la docente, los indicadores del dominio matemático de un/a estudiante serían: tener autonomía (“resolver solo y sin ayuda”) y, en el mejor de los casos, “ayudar a los demás”; interpretar y saber armar situaciones problemáticas (“los cinco pasos que tenés que saber”); resolver operaciones y leer una consigna e identificar errores (“concentración”).
Sus instrumentos de evaluación son las pruebas escritas, pasar al pizarrón para resolver ejercicios y realizar trabajos prácticos en clase o domiciliarios. La correcta resolución de estas actividades serían indicadores del dominio matemático, siendo la resolución de problemas un tema prioritario para 6to año: “hago hincapié en eso, en las resoluciones de los problemas. (...) cómo lo hizo, qué es lo que tuvo en cuenta, cuáles son los datos. (…) voy más al desarrollo que al resultado” (D 6to EP Mate C1, entrevista, 14 de junio de 2017).
A continuación, se ilustra una de las formas de evaluar de la docente. El evento evaluativo consiste en la toma de una prueba escrita en clase, individual y sobre cálculos combinados, en la que los/as estudiantes deben resolver 10 ejercicios:
Figura 1
Instrumento de Evaluación de Contenidos Matemáticos de 6to año Nivel Primario
Nota. En este diseño, la docente propuso 10 ejercicios, cada ejercicio valía un punto y, para aprobar con 7 puntos, el/la estudiante requería haber realizado bien el 50 % de los ejercicios.
Al presentar la consigna al curso, la docente señala: “¿Qué voy a tener en cuenta acá? El procedimiento” y agrega: “todo lo estuvimos practicando, no hay nada raro. Más sencillo que lo que estuvimos viendo. Me interesa cómo lo desarrollan más que el resultado”. Les pregunta: “¿Qué tengo que saber?”, el curso contesta: “las tablas”. Luego, les aconseja: “Separo en términos primero…” y les muestra un ejemplo. (Registro de Observación de evento evaluativo Matemática 6to año primaria del caso 1 (en adelante Reg. Obs. Mate 6to EP C1), 28 de agosto del 2017)
La consigna es familiar para los/as estudiantes y no contaban con material de apoyo para su resolución. La actividad matemática propuesta es una tarea de cálculo, cuya técnica pone en juego una resolución mecánica (“chicos, lo que está dentro del paréntesis no se separa”) que implica la interpretación de los signos matemáticos (“No es multiplicar, esto es un signo de menos, resto”). Sin embargo, se advierte que potenciación y radicación no son contenidos por ser evaluados según el DC (ver Anexo).
Las intervenciones docentes, al momento de la toma de la prueba, van en esa línea: son orientaciones directivas que buscan el dominio matemático procedimental del estudiante (“¿Cuántas veces tienen que multiplicar?”; “Cuál es la raíz cuadrada de 16”; “De dónde saqué el 16, 4x4x4 no da 16) y su autocontrol comportamental (“¿qué tenés que poner acá? ¿Cómo era? … Si llorás no vas a progresar. ... no llores, porque así no puedo ayudarte”; “Chicos, vamos, al otro sexto le di una hora nomás”) (Reg. Obs. Mate 6to EP C1, 28 de agosto del 2017).
La docente considera que un/a estudiante no se puede ir de sexto sin saber:
Primero, (…) las tablas. Es elemental. (…) las cuatro operaciones básicas, la numeración, la descomposición de las tres maneras posibles. Los conceptos básicos de geometría: las figuras, sus clasificaciones y llegar a perímetro y superficie. Fracciones y las cuatro operaciones, cómo se puede hacer y todo eso… y mucho dictado. (D 6to EP Mate C1, entrevista, 14 de junio de 2017).
Llama la atención que los contenidos matemáticos, puestos en juego en la evaluación sumativa registrada, y que forman parte del proceso de calificación y acreditación del dominio del/la estudiante, no forman parte de los contenidos mínimos que la docente considera prioritarios para la acreditación del año.
Finalmente, respecto a la calificación y acreditación, dice que, en el primer trimestre, no hay desaprobados, no por un criterio institucional, sino personal: “si yo desapruebo a un chico en el primer trimestre, puedo perjudicar su autoestima” y, cuando tiene que aplazar, siempre pone a partir de 5 puntos: “Si vos aplazas a un alumno, no sabés en qué condición está en ese momento para recibir esa calificación, no sabes cuál es la reacción de la familia. El chico te puede tomar bronca (…) etc.”. Para calificar cada trimestre, “hay todo un proceso que vos estás evaluando… y decís bueno sí le da o no la nota pero en realidad vos estás teniendo en cuenta todo el proceso desde el primer trimestre del alumno”. En cada trimestre, hay “entre cinco y seis notas. Siete, si es mucho”; dentro de esas notas, también está el trabajo en clase y la responsabilidad y, al momento de acreditar, hay dos motivos por los que un chico puede no aprobar 6to año: “Por incumplimiento: que no haya venido a las pruebas y no me haya justificado; que no esté trabajando; que se haya dedicado a portarse mal (…). Y que haya adquirido el contenido y no le vendría mal hacer un repasito” y, en estos casos, el docente decide enviar al/a la alumno/a a mesa de examen de diciembre o febrero. (D 6to EP Mate C1, entrevista, 14 de junio de 2017).
A partir de lo planteado, la selección de contenidos prioritarios para finalizar 6to año evidencia condiciones propicias para una transición hacia el nivel siguiente. Enfatiza en el control comportamental de la situación de evaluación, la autonomía y colaboración entre pares para la resolución de los cálculos y la lectura de las situaciones problemas como asuntos para tener en cuenta al momento de evaluar. En cuanto a sus formas de calificar y acreditar, busca contemplar las particularidades y acompañar el proceso (plantea actas de compromiso, no aplazar en el primer trimestre, etc.).
En este sentido, se podría observar que, si bien Juan egresa de la primaria pensando que matemática implica “practicar, repasar y saber las tablas”, no es todo lo que ha vivenciado. Fue evaluado con distintos instrumentos, con el propósito de leer bien las actividades, cumplir con los tiempos establecidos y trabajar en el autocontrol durante la situación escolar (responder de modo adecuado a lo que espera el docente en las instancias de evaluación y el trabajo en clase); y, sobre la actividad matemática propiamente dicha, la correcta resolución de los ejercicios o problemas, así como recordar las tablas, garantizó su acreditación en esta asignatura.
El inicio de la escolaridad secundaria
Para los/as estudiantes de primer año, Matemática es vista como una de las materias “más difíciles”. De un total de 201 estudiantes consultados[21], el 32.84 % dice que Matemática es la que más cuesta, seguida de Prácticas del lenguaje (PDL), con 16.92 %, e Inglés, con 11,94 %. También piensan que, al momento de ser evaluados/as, las formas de preguntar y responder, los temas y los tiempos disponibles son más complejos que en primaria.
Juan comenzó su primer año del secundario y está transitando su último trimestre. De su escuela primaria, ingresaron 61 chicos/as[22] y 16 están en su curso. A diferencia de la primaria, la profesora de Matemática, con 22 años de antigüedad docente, es titular, hace 17 años que trabaja en la escuela y es conocida por su exigencia a la hora de enseñar y evaluar.
Al momento de entrevistar a la docente (en el tercer trimestre), comenta sus expectativas al recibir el curso. Comenzaron viendo Estadística:
El tema era interesante, además ellos formaban parte, hacía alguna encuesta, gráficos… pero cuando fuimos a la parte de números [ríe], muerta. No separaban en términos, no sabían las tablas, no sabían sumar. Pero seguía siendo lo mismo!! Si cuando me sacaban un promedio, me lo sacaban bien. ¿Por qué cuando les doy la cuenta así, por separado, no me lo hacen? Yo no sé… (…) a este curso les cuesta la parte de números, fracciones. También les costó la parte de geometría. (...) [entonces] vas seleccionando ejercicios de primaria para que te sigan, porque a veces traes de otros lados suponiendo que van a poder y no pueden. Por ejemplo, sacar perímetros, vos decís… lo tienen que saber y no saben el concepto. A primero vienen chicos de esta escuela [haciendo referencia a la de Juan] y de otras escuelas del distrito y me encuentro que por ahí (…) cuando hago el diagnóstico, los chicos no tienen ni idea de un ángulo. Entonces (…) fui dejando de lado algunas actividades. (…) me llamó la atención que en la división ellos la hacen con la suma. Yo les pregunto cómo saben hacer la división y depende de lo que ellos me digan, hago de una suma y de la otra. Hago de las dos. (...) en primero no me resulta [el uso de la calculadora], porque ellos no saben cómo manejarla. Y ante la desesperación, te ponen cualquier resultado. (...) [Tampoco] saben restar. Cuando tienen, no sé, cero menos tres [hace referencia a números enteros negativos], ellos no sé cómo hacen, pero siempre ese cero menos tres, les queda tres. Y las tablas, tampoco las saben (...) tengo toda la pared (…) con todas las tablas pegadas. Porque cuando estuve trabajando con la parte de divisibilidad no podía avanzar y lo que hice fue pegar las tablas para que levanten la vista y lo miren para la evaluación. No resultó, porque la verdad no resultó. (…) Supongo que de tanto mirarlas, las van a aprender. [otro de los problemas que advierte] es justificar cómo lo hacen. Lo hacen oralmente y a veces les digo: bueno, eso que me están diciendo llevalo al papel. Les cuesta eso. Oralmente lo hacen, el problema es escribirlo. (Docente 1er año secundaria matemática del caso 1 (en adelante D 1ero ES Mate C1), entrevista, 2 de noviembre 2016)
La docente encuentra una distancia entre lo que recibe y lo que espera encontrar, algo semejante a lo que le pasaba a la docente de primaria, también un desconocimiento sobre lo que sus estudiantes vieron los años anteriores. Así, la transición primaria-secundaria no está exenta de los problemas que hay al interior del propio nivel entre años de escolaridad; y, para lograr sus propósitos de enseñanza, la docente toma algunas decisiones: selecciona contenidos, recupera ejercicios de primaria, deja información disponible en el aula (tablas) para que los/as estudiantes puedan apoyarse, aunque reconoce que estas estrategias tampoco son eficaces. Esta situación plantea algunos interrogantes sobre el modo de recuperar los conocimientos matemáticos de los/as estudiantes. ¿Es un problema de estrategias? ¿Refiere a un modo de concebir la enseñanza de la matemática? Los planteos que suscita el análisis de la transición primaria-secundaria circunscriben el debate en el campo de la didáctica de la matemática e interpela los desafíos que tiene el docente ante el trabajo con la diversidad (Lerner, 2007).
A su vez, las expectativas que tiene la docente de primer año, respecto al dominio matemático, requieren complementarse con el estudio de otros casos, ya que lo que ella espera (números enteros negativos, uso de la calculadora, saber justificar por escrito, etc.) no serían contenidos de 6to de primaria, sino de primer o segundo año del secundario. De confirmarse esta observación, podría estar sucediendo lo que la docente de 6to de primaria observaba sobre la transición:
Nuestros alumnos terminan sexto y no séptimo. [Cuando] la secundaria [reconozca esto] va a mejorar. Porque a nuestros alumnos les falta un año [séptimo]. (...) Llegan allá y les dicen: tienen que hacer esto. No lo sé. Y no. Si yo en sexto no tengo para darle ese contenido. (…) Hay un desfasaje grande [entre primaria y el ingreso a primer año]. Dan como sabido los temas. (D 6to EP Mate C1, entrevista, 14 de junio de 2017)
Sobre las evaluaciones, la docente de secundaria tiene consideraciones particulares, cuando trabaja en primer año: “machete autorizado para la evaluación”, que lo confeccionan el mismo día del examen, con todos los contenidos y es sorpresa, porque la idea es que antes “se sienten a practicar”. También lleva impresa la evaluación para que les “sea más sencillo para ellos” y las actividades consisten en:
Primero, les doy un trabajito en clase, similar a lo que puede ser una evaluación. Por ahí, hay dos ejercicios o dos problemitas. (...) Después, hago una evaluación de a dos. A veces, hago evaluación a carpeta abierta. Para que ellos se vayan dando cuenta qué es lo que yo quiero. Y antes de cerrar el trimestre, tomo evaluación. Carpeta cerrada, les dura una hora, cinco ejercicios, les explico cuánto vale cada uno. Les explico todo. (...) Siempre me resulta muy mala la primera evaluación (…) al principio, los dejo armar las parejas, pero después lo que trato de hacer yo: miro el cuadernillo con mis notas y los junto por las notas. (…) Depende de lo que quiera. Si yo veo que es una evaluación para cerrar trimestre, sí. Pero si es otro trabajo, no. (D 1ero ES Mate C1, entrevista, 2 de noviembre 2016)
Respecto a los momentos en que toma la evaluación, los va decidiendo sobre la marcha, dependiendo de lo que vea en clase. Aunque reconoce que, habitualmente, confunde entre lo que cree que pueden los/as chicos/as y lo que efectivamente da cuenta la actividad de evaluación. Por eso, también ha dejado de tomar recuperatorios
Los planteaba más sencillo y me fui dando cuenta... [que] resulta todo lo contrario. Me pasó varias veces, entonces decidí no tomar recuperatorio. Voy tomando siempre una evaluación que incluye temas anteriores, lo voy haciendo así, voy remarcando en clase, con lo que se equivocaron y todo. (D 1ero ES Mate C1, entrevista, 2 de noviembre 2016)
Una de las primeras diferencias que se podría señalar entre la docente de primaria y la del secundario son las formas de evaluar. Mientras, para la primera, la evaluación sumativa es una instancia más del seguimiento, para la segunda, este tipo de evaluación es la principal vía para el seguimiento de los aprendizajes. De modo tal que hace intervenciones para acompañar y formar a los/as estudiantes en el dominio de esta actividad y llegar a ese momento, con cierta autonomía para manejarse en la situación de evaluación. Esta observación, concuerda con el análisis realizado sobre los regímenes académicos y las diferencias entre primaria y secundaria en la relación al evaluar y calificar.
Si bien un docente de secundaria tiene en cuenta diferentes trabajos de los/as estudiantes, la evaluación sumativa (escrita, individual o en parejas) sería el componente central de la acreditación. De este modo, un/a estudiante, en su transición hacia la secundaria, deberá enfrentar un salto cualitativo sobre los criterios que se tienen en cuenta para acreditar una asignatura.
Al registrar el desarrollo de un evento evaluativo, la docente comenta que hace intervenciones para ayudar a los/as estudiantes:
A veces ellos terminan y se quedan con la hoja. Y yo les digo: “si terminan, me la entregan”. Porque puedo visarles… digo: volvé a hacer esta parte, volvé a leer acá, mirá esto, volvé a pensar y se las devuelvo. [les recuerda] poner nombre y apellido, poner la fecha. Y les recomiendo siempre “ustedes traten de pegar la consigna al final así la tienen en la mano, les va a resultar más fácil para la lectura (y evitar problemas de distracción)”. Les digo: empiecen a resolver. Empiecen a resolver por lo que les resulta más sencillo. Vuelvan a leer toda la evaluación. No interesa el orden, mientras esté todo resuelto (...) Todas esas pautas, se las aclaro. La primera evaluación, la segunda evaluación. Y lo que trato no hacer es explicarles las evaluaciones. Porque la consigna forma parte de la evaluación. (Registro de Observación de evento evaluativo Matemática 1er año secundaria del caso 1 (en adelante Reg. Obs. Mate 1ero ES C1), 16 de noviembre del 2016)
El evento evaluativo comenzó luego de un repaso sobre representación gráfica y comparación de fracciones, a partir de un trabajo práctico que había dejado la semana anterior. En el intercambio, una estudiante le consulta cómo se multiplica una fracción y la profesora escribe una fracción cualquiera (no de las que forman parte de la consigna de examen) en el pizarrón y comienza a preguntarles: “¿Qué es lo primero que se debe hacer?” y lo resuelve (todas las resoluciones serán conjuntas con el grupo de estudiantes). Luego, avanza explicando con otro ejemplo la división de fracciones y consulta al curso: “¿Por qué el resultado es una fracción impropia? ¿Cómo se produce un número mixto?”. Después, pregunta:
“¿Qué más? ¿Alguna otra duda?”,
“La raíz”, contesta una estudiante. La docente escribe un ejemplo cualquiera: 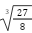 y pregunta: “¿Qué número
multiplicado tres veces me da 27?”. Luego, señala: “recuerden que multiplica los
índices”. La profesora escribe
y pregunta: “¿Qué número
multiplicado tres veces me da 27?”. Luego, señala: “recuerden que multiplica los
índices”. La profesora escribe 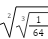 y
conversa con los estudiantes sobre su resolución. Entonces, presenta:
y
conversa con los estudiantes sobre su resolución. Entonces, presenta: 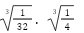 y la resuelven conjuntamente. De nuevo, consulta:
“¿Alguna otra duda?”, “la potencia”, dicen los estudiantes, y la profesora
escribe otro ejercicio
y la resuelven conjuntamente. De nuevo, consulta:
“¿Alguna otra duda?”, “la potencia”, dicen los estudiantes, y la profesora
escribe otro ejercicio 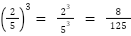 . Reitera: “¿Otra
duda?” y los estudiantes dicen: “¿Cómo se ubica en la recta
numérica?” y la profesora lo explica dialogando con los estudiantes. Reitera:
“¿Alguna otra pregunta?”, un estudiante pregunta: “¿Potencia de
potencia?” y van armando la explicación entre varios. Reitera: “¿Algo
más?” y dice una estudiante: “La de las 2 raíz”, “Eso se lo
expliqué recién a Sofía” dice la profesora, y la estudiante responde:
“Sí, pero no entendí”. Entonces, lo vuelve a explicar. Finalmente, la docente les
presenta la consigna del trabajo práctico y les dice: “No les voy a tomar una
‘evaluación, evaluación’, pero yo necesito una nota de estos temas”
y les presenta la consigna, les pide que armen los
grupos y les recuerda que pueden usar la carpeta. (Reg. Obs. Mate 1ero ES C1, 16 de noviembre del
2016)
. Reitera: “¿Otra
duda?” y los estudiantes dicen: “¿Cómo se ubica en la recta
numérica?” y la profesora lo explica dialogando con los estudiantes. Reitera:
“¿Alguna otra pregunta?”, un estudiante pregunta: “¿Potencia de
potencia?” y van armando la explicación entre varios. Reitera: “¿Algo
más?” y dice una estudiante: “La de las 2 raíz”, “Eso se lo
expliqué recién a Sofía” dice la profesora, y la estudiante responde:
“Sí, pero no entendí”. Entonces, lo vuelve a explicar. Finalmente, la docente les
presenta la consigna del trabajo práctico y les dice: “No les voy a tomar una
‘evaluación, evaluación’, pero yo necesito una nota de estos temas”
y les presenta la consigna, les pide que armen los
grupos y les recuerda que pueden usar la carpeta. (Reg. Obs. Mate 1ero ES C1, 16 de noviembre del
2016)
Figura 2
Instrumento de evaluación de contenidos matemáticos de 1er año nivel secundario
También les aclara que, a pesar de trabajar en parejas, cada uno/a debe entregar su hoja y agrega: “Yo no respondo nada. Tienen tiempo hasta el recreo. Entregan las parejas juntas, no me entrega primero uno y luego el otro”. (Reg. Obs. Mate 1ero ES C1, 16 de noviembre del 2016)
Un alumno consulta por la expresión decimal y la docente dice que no va a responder, que busque en la carpeta. Otra alumna pregunta:
“¿Se puede buscar en la carpeta?” y responde “Es lo que les digo”. Luego, agrega: “A ver chicos. Todos me preguntan por el punto 2. ¿Qué significa representar? ¿Qué significa expresión decimal? Yo lo escribí en el pizarrón así que agarren las carpetas y encuéntrenlo”. Al entregar la primera pareja, la docente mira y les dice: “El punto 1 dice responde y justifique. ¿y qué escribieron ustedes? sí, no. ¿Eso es justificar? ¿Por qué ‘sí’? ¿Por qué ‘no’? Y miren acá [les señala un cálculo mal hecho]”. Luego, aclara a todo el curso: “Que nadie se olvide la raya de fracción porque no corrijo”. (Reg. Obs. Mate 1ero ES C1, 16 de noviembre del 2016)
La consigna combina tres tipos de tareas: resolución de problemas, representación gráfica y resolución de cálculos. A diferencia de primaria, donde el instrumento se focaliza en un tipo de tarea, aquí, el instrumento presenta tres tipos de tareas diferentes y la técnica no se reduce a la aplicación de un mecanismo de resolución, conlleva también un acto interpretación y de argumentación, así como un pasaje de una forma de representar a otra (número a gráfico, número a expresión equivalente) y, si bien, en la actividad de evaluación, la carpeta tendrá la función de mediar la asistencia o apoyo que requieran los/as estudiantes, su disponibilidad no implica un acceso al conocimiento matemático[23].
Al terminar la evaluación, se le consultó a algunos/as compañeros/as de Juan cómo les había resultado la actividad. En su mayoría, respondieron que eran temas vistos, que las actividades eran más o menos fáciles (aunque tuvieron dificultades en algunos de los ejercicios) y que consideraban que se sacarían entre 7 u 8 puntos, aunque posteriormente sus calificaciones fueron inferiores. (Reg. Obs. Mate 1ero ES C1, 16 de noviembre del 2016)
En la devolución general, la docente hizo las siguientes observaciones:
Vi muchos problemas con el “represente” y “clasifique” [se refiere a la consigna 2.a]. ¿Qué quiere decir “represente”?; yo no sé si se entusiasmaron con los ejercicios y no leyeron bien las consignas. ¿Qué es clasificar? Cuando decía “halla la expresión decimal” [consigna 2.b.], ¿qué había que hacer? El “ubique en la recta numérica” [2.c] la mayoría lo hizo bien. (…) La consigna dice “responde y justifique” [consigna 1]. Muchos responden, pero nadie dice el por qué. ¿Poner “sí” o “no” es justificar? Nadie responde el “por qué”. Por ejemplo, ustedes cuando llegan tarde me dicen “profe llegué tarde porque… (…) Fracciones equivalentes lo tenían claro. En 1.b, ¿qué tenían que hacer? Si dice “simplifico”, ¿qué tienen que hacer? Varios alumnos dicen: “Simplificar, profesora”. ¿Y por qué no lo hicieron? Uno solo lo hizo. Después el número mixto lo saben pasar todos a fracción. Los cálculos combinados la mayoría los hizo bien, por eso hoy les tomo oral porque sé que saben. (Registro Observación de la devolución evento evaluativo de matemática 1er año secundaria del caso 1 (en adelante Reg Obs. devolución. Mate 1ero ES C1), 21 de noviembre del 2016)
En su devolución, despliega los criterios que tuvo en cuenta al corregir. Espera que sus estudiantes argumenten el por qué de un planteo o una resolución, muestren la manera de pensarlo y se detengan en una lectura atenta de la consigna. Si bien la lectura de la consigna es algo que se inició en primaria, en secundaria se suman nuevas demandas cognoscitivas en el dominio matemático: la interpretación, su argumentación o contraargumentación, que no fueron planteadas en la experiencia de primaria.
Juan es llamado por la profesora para cerrar la nota del tercer trimestre y le dice sobre su evaluación:
Tu evaluación no está tan mal, tenés un 6. Te equivocaste en bajar los ceros. Los cálculos del punto 3 están bien. En la consigna 1 te faltó justificar (…) La verdad muy bien en este trimestre. ¿Vos necesitabas un 8? (Reg Obs. devolución. Mate 1ero ES C1, 21 de noviembre del 2016)
Juan contesta que sí. Entonces, mientras cierra la nota del trimestre, le pide a Juan que saque el promedio de los tres trimestres.
Juan aprobó el tercer trimestre con 7 puntos y pasará el año próximo a 2do. Está contento, pero sabe que hay varios que tienen algunos problemas, como el caso de Franco. Este tuvo, en el primer y segundo semestre, 5 y 7, respectivamente. Y, en esta evaluación, no le había ido bien. Había hecho pareja con Walter, un chico que, según la docente, “es hereditario [porque sus hermanos también tenían el mismo problema] (…) estudia, pero no le alcanza el tiempo” (Reg Obs. devolución. Mate 1ero ES C1, 21 de noviembre del 2016), habían llegado a hacer solo el punto 1. a) y b) y él intentó hacer el 3. a). Sin embargo, ambos tuvieron un 2 en la actividad. Los días anteriores, Franco había faltado a clase porque viajó a un festejo familiar; al regresar, no entendía lo que estaban dando y estaba próximo el trabajo práctico. Había pedido la carpeta, pero no entendía y, cuando le consultó a la profesora, según Franco, esta le dijo “Que no me iba a explicar, porque ella no fue la que faltó”. (Estudiante 1er año secundaria sobre evento evaluativo matemática del caso 1(en adelante Est 1ero Eva Mate C1, entrevista, 23 de noviembre del 2016)
El día del trabajo práctico, él no tenía la carpeta completa, dice que sumar, multiplicar o dividir lo entiende, pero cuando aparecen los paréntesis no entiende nada y, si bien la actividad fue a carpeta abierta y con un compañero, en su carpeta no tenía nada “con paréntesis” y cálculos combinados y su compañero “tampoco estudió y no quería revisar la carpeta”. Sobre lo que Franco termina reflexionando: “En la primaria, nos explicaban uno por uno o si no, todos juntos [y] a los que no entendían, levantaban la mano y ahí, la profesora iba y le explicaba. Ahora, solamente le explica a todos juntos y ya está” (Est 1ero Eva Mate C1, entrevista, 23 de noviembre del 2016). Para Franco, la secundaria cambió las reglas de mediación y sostén, y la atención personalizada no está disponible ⎯por lo menos con esta docente⎯. Juan confía en que Franco, en la semana de orientación, pueda alcanzar lo que necesita. El tercer trimestre lo cerró con 6 y sabe que la docente está predispuesta. El objetivo es pasar de año y lo que entiende de Matemática es el medio para lograrlo. (Est 1ero Eva Mate C1, entrevista, 23 de noviembre del 2016)
Finalmente, respecto a las calificaciones y acreditación, la docente dice:
Ellos saben que todo lo que me llevo a casa, le pongo nota. Después, cuando voy a cerrar el trimestre, me fijo. A veces, saco nota de trabajos en clase, hago solo una nota. De las evaluaciones, también. Y después, le escribo una nota de promedio. Que con esto que insisto yo, de pasar al pizarrón, de participar en clase, de ayudar al compañero… eso les sirve (…) ellos saben clarito de dónde yo saco la nota. (…) les digo a los chicos, “si te fue mal en el primer trimestre, bueno. No llegamos con la nota, (…) te puedo llegar a escribir el diez, que vos necesitás. (…) Si veo el esfuerzo y vos te sacás: seis, siete en las evaluaciones. Yo le voy a escribir el diez”. (D 1ero ES Mate C1, entrevista, 2 de noviembre 2016)
La carpeta no la corrige, solo las pide en la semana de orientación: “Para que, por lo menos, se sienten a completar la carpeta” y, respecto a la corrección, precisa que, en las evaluaciones, los ejercicios tienen jerarquías para la asignación de una calificación:
Ellos muchas veces lo saben, porque me preguntan cuánto vale cada ejercicio. Depende de lo que esté tomando. Yo jerarquizo siempre los ejercicios. Cuál vale más, cuál vale menos. Y a veces se los digo. Otras veces, no. Habitualmente corrijo y pongo la nota final (…) depende de la dificultad del enunciado, jerarquizo (…) leo la consigna y leo lo que ellos me escriben. Si está dentro de lo que él entendió y lo puede explicar, va a estar bien. (D 1ero ES Mate C1, entrevista, 2 de noviembre 2016)
El esfuerzo es un criterio de acreditación tanto en primaria como secundaria, pero particularmente en este último nivel, refleja las transformaciones que fueron produciéndose en el nivel secundario, con la ampliación de la matrícula y las dificultades en el trabajo con la diversidad y la enseñanza de los contenidos escolares (Falconi, 2015, 2014). Sin embargo, estos efectos por la ampliación no solo lo padece la actividad docente, los procesos de subjetivación de los/as estudiantes también, focalizando su atención en el promedio más que en el dominio del saber en juego.
La preocupación de estos/as últimos por la calificación trimestral y su promedio es algo que se evidencia en la escuela secundaria. La actividad matemática no puede escindirse de los motivos, es decir, del objetivo o resultado que se intenta obtener al momento de su realización y estos direccionan las operaciones de los/as estudiantes.
Charlot (2014) lo ilustra con claridad:
Cuando el alumno estudia matemática para pasar de grado u obtener un diploma, esa no es una actividad, la actividad es pasar de grado. En ese caso, estudiar matemática es una operación en la actividad para pasar de grado. Ahora bien, cuando estudia matemática porque le gusta, ahí se transforma en una actividad. En nuestras aulas los estudiantes realizan más operaciones que actividades, muchas veces ellos no llevan a cabo una actividad al estudiar, sino una operación que tiene un objetivo diferente del motivo. Cuando existe una coherencia entre motivo y objetivo hay una actividad, cuando no la hay, no estamos desarrollando una actividad intelectual sino una operación para otra actividad. (p. 28-29)
La actividad matemática que se ofrece a los/as estudiantes se articula con las transformaciones cognoscitivas que ésta demanda para su dominio. Sin embargo, si lo que se ofrece reduce la actividad a una serie de tareas donde el sentido queda suspendido, ahí, se corre el riesgo de la discontinuidad de los aprendizajes y, con ello, el riesgo de hacer de la matemática una operación (una carrera de obstáculos) al servicio de lograr un pasaje exitoso por el sistema.
Comentarios finales
Se partió de la hipótesis de que algunos problemas para lograr tránsitos sostenidos, continuos, completos y con aprendizaje relevantes por el sistema escolar, podrían relacionarse con la heterogeneidad y discontinuidad de criterios y modalidades de evaluación sumativa en los distintos niveles educativos. A partir del análisis de una trayectoria plausible en la transición primaria-secundaria en el área de matemática, se pudo dar cuenta de lo complejo y multidimensional que es la variable “transición”.
En el pasaje del nivel primario al secundario, no solo hay un cambio en el régimen académico, sino criterios de evaluación y acreditación propios de cada nivel que requieren ser analizados en conjunto si se busca, en el marco de la ampliación de los derechos a la educación, lograr tránsitos sostenidos, continuos y completos.
El análisis realizado en torno al área de matemática, si bien es limitado en su alcance y requiere ser complementado con otros estudios de caso, ha permitido dilucidar varios asuntos. Por un lado, sostenemos la importancia que tiene, para el campo de la investigación educativa, resituar los problemas de análisis contemplando el rol que juegan los objetos de conocimiento en los procesos de enseñanza y aprendizaje escolares (Castorina y Sadovsky, 2021). Mirar las prácticas docentes, en este caso la evaluación de los aprendizajes a la luz de los objetos de enseñanza, permite captar con mayor claridad los problemas que surgen al momento de la transmisión del saber. Charlot (2014) dice:
A partir del momento en que se abre la escuela a nuevos tipos de alumnos, la escuela entra en contradicciones, la escuela comienza a ser atravesada por contradicciones profundas, estructurales. Es interesante advertir que cada vez que nuevos tipos de alumnos ingresan en una parte del sistema escolar, esa parte entra en “crisis”. Ha pasado en el siglo XIX en la escuela primaria, después en la enseñanza secundaria, ya comenzó a suceder en la enseñanza superior. Debemos reflexionar sobre la forma en que reaccionamos: si queremos una escuela tranquila, calma, vamos a tener que aceptar la selección en la entrada; si queremos una escuela abierta, más democratizada, va a estar atravesada por contradicciones profundas. Tenemos que entender que los profesores generalmente quieren la democratización de la escuela, pero también es necesario asumir que la primera consecuencia de esa democratización es que las contradicciones entran en el salón de clase, por lo tanto el éxito democrático político se evidencia en problemas pedagógicos. (p. 24)
Así, el problema de la transición primaria-secundaria tiene algunas particularidades, pero también un denominador común: “pasar de grado” o “de nivel” encierra el desafío de superar los reduccionismos que rigen en las prácticas de evaluación. Reducir la evaluación a la calificación y esta última, a una valoración del esfuerzo de los/as estudiantes, más que a su dominio de conocimiento, no puede ser la alternativa frente a la ampliación de la matrícula.
A su vez, este problema encierra otro, el restituir el sentido de la actividad matemática en el funcionamiento del sistema educativo. El/la estudiante hace lo que el docente habilita y, si repetir contenidos es la propuesta docente frente al problema de la recuperación de los aprendizajes, es necesario trabajar en el desarrollo de estrategias que habiliten el recordar y reelaborar más que el repetir (Napp et al., 2005; Helman, 2020). El señalamiento apunta a pensar el trabajo docente en torno a estrategias para enlazar, coordinar e integrar aprendizajes producidos en distintos momentos por parte del/la estudiante bajo la coordinación del docente (Terigi, 2015; Lerner, 2007). Habilitar al docente a poner palabras a la “falta de entendimiento” del estudiantado (y su proceso de conceptualización) para lograr una continuidad en las posibles discontinuidades del sistema.
Hay discontinuidades que son asuntos de política curricular, por ejemplo, el equilibrio curricular entre niveles, respecto a la definición de las expectativas de logro y la evaluación. Esto requeriría de acuerdos sobre las formas y el sentido de la evaluación de los aprendizajes en el área de la matemática, asumiendo el problema común del área, que es evitar que la matemática sea reducida a la resolución mecánica y memorística de las operaciones. También hay discontinuidades a nivel de la organización escolar, a partir del análisis de los regímenes académicos: la relación evaluar-calificar requiere de acuerdos comunes entre niveles para promover las transiciones y, finalmente, hay discontinuidades en las prácticas de evaluación de los aprendizajes en el área de la matemática, principalmente entre lo que se enseñanza y lo que se evalúa (autonomía en la resolución de cálculos, leer e identificar errores, interpretar consignas, argumentar, contraargumentar, etc.). Tanto en primaria como en secundaria, los indicios que toman los/as docentes para evaluar el dominio del conocimiento matemático pareciera no ser materia de enseñanza. Desde nuestro punto de vista, esta diferencia es posible si se comprende a la matemática no sólo como campo conceptual, sino también como un sistema de representación externo. Es decir, un sistema de instrumentos culturales semióticos, creados a lo largo de la historia de la humanidad, y que está al servicio de un modo de analizar y comprender el mundo (Martí, 2012). En esta línea, no se puede escindir el dominio del sistema externo del conceptual, entre ellos hay una relación recíproca y, en materia de apropiación y desarrollo, implica el pasaje de un uso manipulativo y convencional (uso pragmático) o un significado simbólico, conceptual (uso epistémico) (Perez-Echeverria et al., 2010): “No se puede lograr una comprensión conceptual de los sistemas (externos) sin que haya cierto grado de conocimiento del código y la sintaxis, pero el aprendizaje (dominio) de esos aspectos no es ajeno de los contenidos que le confieren significado” (p. 142).
Se considera que advertir esta distinción-relación colaboraría a comprender la compleja tarea de enseñar matemática. Los procesos educativos son básicamente procesos de función comunicativa, orientados al dominio y control creciente de funciones cognitivas que se transforman por el contacto con los diferentes sistemas externos de la cultura (Riviere, 2002). Y, a lo largo del sistema educativo, se espera un cambio psicológico en los/as estudiantes (Martín, 2005), es decir, un cambio en las formas de comportarse, pensar y conceptualizar a partir del dominio de dicho sistema de representación.
Si bien este trabajo necesita avanzar en los estudios de casos del resto de las transiciones plausibles que comprendió el estudio marco, al mismo tiempo, permite delinear algunos de los problemas en el estudio de las transiciones escolares y las continuidades y discontinuidades de las trayectorias escolares.
De la serie Rakulche, acrílico. Rosana Moreno
[1] PICT 2014-0898. Transiciones educativas primaria/secundaria y secundaria/superior: trayectorias escolares y evaluación de aprendizajes. Investigadora responsable: Flavia Terigi, con sede en el Instituto de Desarrollo Humano de la Universidad Nacional de General Sarmiento. Desde abril de 2016 a septiembre de 2019.
[2] “Trayectorias escolares y evaluación: las prácticas de evaluación sumativa en las transiciones entre niveles educativos” bajo la dirección de Dra. Silvina Cimolai y la codirección de la Dra. Flavia Terigi.
[3] Definimos trayectos plausibles a una proyección posible, de un/a estudiante hipotético/a, por el sistema escolar, a partir de información aportada por las instituciones educativas que participaron en el estudio.
[4] El CAU fue una política de ingreso a la UNGS entre los años 1995 y 2018 y buscaba facilitar la transición del/de la estudiante entre la escuela secundaria y la universidad (Res CS 4621/13).
[5] Se analizaron los datos entre 2012 y 2015 y se seleccionaron las escuelas comprendidas en la Región Educativa IX (comprende los partidos de Malvinas Argentinas, San Miguel, Moreno y José C. Paz).
[6] De las seis escuelas secundarias, dos, por características de ubicación o procesos de conformación de matrícula, no permitieron identificar una escuela primaria que proveyera el mayor número de su matrícula.
[7] Un evento evaluativo es una actividad de evaluación sumativa definida por un/a docente. Comprende las decisiones tomadas acerca de qué, cómo y cuándo evaluar, el diseño o la selección de los instrumentos de evaluación, la instancia de resolución de la actividad por parte del estudiantado, la corrección y calificación por parte del/ la docente y la instancia de devolución a los/as estudiantes.
[8] Comprende información relevante de las escuelas, como, por ejemplo, el registro anual, proyecto de evaluación institucional, programas, etc., así como consultas a documentos de los órganos de gobierno, como los diseños curriculares, régimen académico, documentos de trabajo, etc.
[9] Para el caso del estudiantado del nivel secundario y superior, se administró un cuestionario y, para el estudiantado del nivel primario, se realizaron grupos focales. El objetivo, en ambos casos, fue relevar datos básicos del cuerpo estudiantil y sus opiniones sobre la evaluación, calificaciones y acreditación.
[10] Sobre contenidos a enseñar, formas de evaluar y expectativas de logro.
[11] En el análisis del evento evaluativo, se tomó en cuenta por un lado, el instrumento que se administró: la familiaridad de la consigna para el estudiantado; la redacción de la consigna (escritura, si hay pistas y cuántas operaciones solicitan); tipografía (manuscrita, del/a docente o alumno/a, o digital); qué tarea (y tipo de tareas) se solicitaba y cómo había que resolverlo (técnica) ⎯la distinción tarea-técnica se toma de Chevallard (1999)⎯; y por otro, las interacciones pedagógico-didácticas del evento evaluativo: presentación de la consigna (indicaciones, sugerencias, y advertencias); condiciones de realización (disponibilidad o no de materiales de consulta, tipo de materiales, anticipaciones docente sobre las condiciones de realización) e intercambios orales que se desarrollan en el evento y en la instancia de devolución.
[12] Sobre las formas de evaluar en el área curricular estudiada y las diferencias entre la primaria y la secundaria.
[13] Los materiales de referencias para este análisis fueron el DC de Segundo Ciclo Educación Primaria, versión 2008, y el DC Educación Secundaria 1er año, versión 2006. Se puede consultar, en el Anexo I, una sistematización de los contenidos que cada diseño contempla para cada año escolar en juego.
[14] En el año 2021, se publicó, en el portal educ.ar, material que avanza en esta línea: https://www.educ.ar/recursos/157797/transiciones-entre-niveles-educativos
[15] Consultar Anexo para ver detalles en las expectativas de logro por niveles respecto del espacio curricular Matemática.
[16] Aunque trabajos del campo de la didáctica de la matemática sitúan que el problema no sería la memorización, sino enfocar la enseñanza en un trabajo gradual y progresivo de abstracción por parte de los/as estudiantes, que no solo se refleje en la secuencia de contenidos o el trabajo en el aula, sino en representación en el campo de la matemática (Bosch et al., 2004; Peganos et al., 2017; Grimaldi et al., 2017).
[17] En este caso, se han tomado en cuenta el Régimen académico de nivel primario (Res DGCyE 1057/14) y Régimen académico del nivel Secundario (Res DGCyE 587/2011). No se tienen en cuenta, en este estudio, las modificaciones sufridas por el contexto de pandemia. No se incluye en la sistematización de estos criterios la normativa vinculada a las mesas examinadoras, así como las pautas que regulan a los/as estudiantes que rinden en carácter de libre debido a que excede el recorte y los propósitos de este trabajo.
[18] Al momento del estudio, la nota de la evaluación integradora es una nota más del último trimestre. Si bien, en un primer momento, se promediaba con la calificación final, esto generó que el estudiantado se llevase la materia y se cambiaron las condiciones de acreditación, en caso de existir esta evaluación.
[19] La vivencia es el modo en que un sujeto, tanto desde el punto de vista afectivo como cognitivo, puede enfrentar una situación particular de la vida social (Baquero, 2012).
[20] Con esta expresión, queremos señalar que son hipótesis que elabora la docente, a partir de las cuales regula su actividad; sin embargo, no podría afirmarse que efectivamente aconteció.
[21] Encuesta a estudiantes de primer año de los 5 casos estudiados. Total de estudiantes consultados: 201.
[22] Total de ingresantes a la escuela según información brindada por el director de la secundaria. Contempla turno mañana y tarde.
[23] La distinción disponibilidad-acceso son retomadas del planteo de Kalman (2003). La disponibilidad refiere a tener los materiales/instrumentos culturales al “alcance de la mano” y el acceso refiere al uso que un sujeto puede darle a dicho instrumento. En este último caso, se ponen en juego disponibilidades cognitivas para ese “saber hacer”.
Referencias
Amantea, A., Armendariz, C. y Feced, L. (junio de 2019). El curriculum ante la expansión de la obligatoriedad escolar. Ponencia Eje 2: Sistema educativo, discontinuidades y desigualdades. III Coloquio de Investigación Educativa en Argentina. Facultad de Ciencias Económicas, UBA.
Baquero, R., Terigi, F., Toscano, A. G., Briscioli, B. y Sburlatti, S. (2009). Variaciones del régimen académico en escuelas medias con población vulnerable. Un estudio de casos en el Área Metropolitana Buenos Aires. Revista Iberoamericana sobre Calidad, Eficacia y Cambio en Educación, 7(4), 292-319. http://www.rinace.net/reice/numeros/arts/vol7num4/art15.htm
Briscioli, B. y Rio, V. (abril de 2018). Inclusión y diferenciación en la transición de primaria a secundaria. Experiencias de articulación entre niveles en escuelas del Conurbano bonaerense. VII Congreso Nacional y V Internacional de Investigación Educativa. Facultad de Ciencias de la Educación, Universidad Nacional del Comahue.
Bosch, M., Fonseca, C. y Gascón, J. (2004). Incompletitud de las organizaciones matemáticas locales en las instituciones escolares. Recherches en Didactique des Mathématiques, 24(2-3), 205-250.
Bruner, J. (2003). La fábrica de historias. Fondo de cultura económica.
Camillioni, A. (1998). Sistemas de calificación y regímenes de promoción. En La evaluación de los aprendizajes en el debate didáctico contemporáneo (pp. 133-176). Paidós Educador.
Camilloni, A. (2014). La responsabilidad social y pedagógica de la evaluación de los aprendizajes. Itinerarios Educativos, (8), 51-64. https://doi.org/10.14409/ie.v0i8.6055
Castorina, J. A. y Sadovsky, P. (2021). El significado de los conocimientos en los procesos de enseñanza y aprendizajes escolares. Ediciones UNIPE.
Charlot, B. (2014). La relación de los jóvenes con el saber en la escuela y en la universidad, problemáticas, metodologías y resultados de las investigaciones. Polifonías Revista de Educación, III(4), 15-35. http://www.polifoniasrevista.unlu.edu.ar/sites/www.polifoniasrevista.unlu.edu.ar/files/site/3%20-%20Charlot.pdf
Chevallard, Y. (1999). El análisis de las prácticas docentes en la teoría antropológica de lo didáctico. Recherches en Didactique des Mathématiques, 19(2), 221-266.
Davini, M. C. (1999). El diseño de un proyecto curricular: construyendo metodologías abiertas. Material de cátedra de la asignatura Curriculum. Licenciatura en Educación, Universidad Virtual de Quilmes.
Elola, N., Zanelli, N., Oliva, A. y Toranzos, L. (2010). La evaluación educativa. Fundamentos teóricos y orientaciones prácticas. Aique.
Falconi, O. (2015). Criterios de evaluación de profesores en una escuela secundaria estatal: La valoración del trabajo, el esfuerzo y la autonomía en la tarea escolar. Cuadernos de Educación, (12). Universidad Nacional de Córdoba, Centro de Investigaciones de la Facultad de Filosofía y Humanidades.
Falconi, O. (2014). La evaluación situada intraclase: un modo de evaluar y calificar en la Escuela Secundaria. En N. Alterman y A. Coria (Coords.), Evaluación y Disciplina Escolar. Nexos, divergencias y autonomía relativa. Editorial Brujas.
Feldman, D. y Palamidessi, M. (2015). Continuidad y Cambio en el Currículum. Los planes para la educación primaria y media en Uruguay. Instituto Nacional de Evaluación Educativa.
Feldman, D., Armendariz, C. y Feced, L. (septiembre de 2017). Curriculum y aumento de la obligatoriedad escolar. VI Congreso Nacional e Internacional de Estudios Comparados en Educación. Inclusión, Calidad y Equidad en la Educación. Pasado, Presente y Futuro en perspectiva comparada. Buenos Aires.
Grimaldi, V., Itzcovich, H. y Novembre, A. (2017). Secundaria Básica y últimos años del nivel primario. En C. Broitman (Coord.), Cuadernos de apoyo didáctico. Santillana.
Lerner, D. (2007). Enseñar en la diversidad. Lectura y Vida. Revista Latinoamericana de Lectura, 28(4). Asociación Internacional de Lectura, Facultad de Humanidades y Ciencias de la Educación, Universidad Nacional de La Plata.
Marti, E. (2005). Desarrollo, cultura y educación. Ed. Amorrortu.
Martí, E. (2012). Desarrollo del pensamiento e instrumentos culturales. En M. Carretero y J. A. Castorina (Comps.), Desarrollo cognitivo y educación, Tomo II. Paidós.
Napp, C., November, A., Sadovsky, P. y Sessa, C. (2005). La formación de los alumnos como estudiantes. Estudiar matemática. Documento 2 serie: Apoyo a los alumnos de primer año en los inicios de nivel medio. Dirección General de Planeamiento. Secretaría de Educación.
Niño, M. F. (2011). El proceso de construcción curricular de contenidos de Estadística en la EGB3 de Misiones. Revista Ciencia y Tecnología, 13(16), 21-29.
Martinez-Rizo, F. (2015). Estudios sobre prácticas de evaluación en el aula: revisión de la literatura. Revista Electrónica de investigación Educativa, 17(1), 17-32.
Parra, C. y Saiz, I. (Comp.). (1997). Didáctica de matemáticas. Aportes y Reflexiones. Paidós.
Penagosa, M., Mariño, L. F. y Hernandez, R. V. (2017). Pensamiento matemático elemental y avanzado como actividad humana en permanente evolución. Perspectivas, 2(1), 105-116. Universidad Francisco de Paula Santander.
Perrenoud, P. (2015). La evaluación de los alumnos. Colihue.
Puy Perez Echeverría, M., Martí, E. y Pozo, J. I. (2010). Los sistemas externos de representación como herramientas de la mente. Cultura y Educación, 22(2), 133-147.
Ravela, P. (2009). Consignas, devoluciones y calificaciones: Los problemas de la evaluación en las aulas de educación primaria en América Latina. Páginas de Educación, 2(1). Departamento de Educación, Universidad Católica de Uruguay.
Ravela, P., Arregui, P., Valverde, G., Wolfe, R., Ferrer, G., Martínez Rizo, F., Aylwin, M. y Wolff, L. (2009). Las evaluaciones educativas que América Latina necesita. PREAL. Disponible en: 200.6.99.248/~bru487cl/files/EVals_AL.pdf [último acceso: 2 de junio de 2014].
Rivière, A. (2002). Desarrollo y educación: el papel de la educación en el “diseño” del desarrollo humano. En A. Rivière, Obras escogidas. Volumen III: Metarrepresentación y semiosis. Editorial Médica Panamericana.
Sadovsky, P. y Lerner, D. (Coords.). (2006). ¿Qué se enseña y qué se aprende en las escuelas de la ciudad de Buenos Aires? Informe final. https://www.buenosaires.gob.ar/sites/gcaba/files/2006que_se_ensena_y_que_se_aprende_en_las_escuelas_de_la_ciudad_de_buenos_aires_0.pdf
Stake, R. E. (2005). Investigación con estudio de casos. Morata.
Terigi, F. (febrero de 2010). Las cronologías de aprendizaje: un concepto para pensar las trayectorias escolares. Jornada de Apertura ciclo lectivo 2010. Conferencia llevada a cabo en la Jornada del Ministerio de Educación y Cultura del Gobierno de La Pampa, Santa Rosa.
Terigi, F. (2014). Trayectorias escolares e inclusión educativa: del enfoque individual al desafío para las políticas educativas. En A. Marchesi, R. Blanco y L. Hernández (Coords.), Avances y desafíos de la educación inclusiva en Iberoamérica (pp. 71-87). Organización de Estados Iberoamericanos/Fundación MAPFRE.
Terigi, F. (2015). Las cronologías de aprendizaje entre las trayectorias escolares y las trayectorias educativas. En Problemas, estrategias y discursos sobre las Políticas Socioeducativas. Seminario II DNPS. Ministerio de Educación de la Nación.
Anexo
Comparativo entre 6to año de Nivel Primario y 1er año de Nivel Secundario sobre contenidos matemáticos y orientaciones para la evaluación
Diseño curricular Segundo Ciclo (Provincia de Buenos Aires) Fuente: Diseño Curricular Segundo Ciclo Educación Primaria_2008
Segundo ciclo
4to, 5to y 6to
Matemática.
Carga horaria: 5 y 6 horas semanales
Marco general para la educación primaria:
Matemática
¿Cómo evaluar la enseñanza? ¿Cómo evaluar los aprendizajes? ¿Es preciso estudiar en matemática? ¿Qué se entiende por “estudiar matemática”? ¿Cómo enseñar a estudiar?
“La evaluación en la escuela permite recabar información para tomar decisiones de manera más racional y fundamentada con la finalidad de reorientar permanentemente la enseñanza. En la gestión de las clases en torno a un contenido, el maestro/a habitualmente releva información sobre el proceso de enseñanza. Utiliza para ello -en diferentes momentos- instancias de trabajo individual o colectivo, producciones de los alumnos/as orales y/o escritas. (…) Se ha señalado la importancia -en el momento de la enseñanza- de una fuerte presencia de problemas ‘nuevos’ que exigen desplegar un trabajo exploratorio. En cambio, en la instancia de evaluación, será oportuno que los alumnos/as se encuentren con problemas ya conocidos (…) Es necesario aclarar que en este diseño curricular se proponen algunos contenidos sobre los que se sugiere realizar un trabajo exploratorio, por ejemplo la escritura de números grandes en los primeros años, la comparación entre sistemas de numeración antiguos, etc. Sobre estos contenidos no se espera una evaluación individual. Este criterio significa instalar la idea de que no todo aquello que se enseña es preciso que sea evaluado individualmente. (…) un objetivo de enseñanza en clase el ‘enseñar a estudiar’. Algunos ejemplos de esta clase de actividades pueden ser las siguientes: releer las conclusiones elaboradas en forma colectiva; rehacer los problemas más complejos; realizar un ‘simulacro’ de evaluación con problemas similares a los que tendrá una prueba escrita; revisar problemas solucionados para reflexionar sobre las estrategias usadas; agrupar problemas ya resueltos en ‘tipos de problemas’; preparar en pequeños grupos ensayos de pruebas con selección de problemas a partir de consultar los realizados en cuadernos o carpetas; elaborar carátulas o folios que permitan ordenar e identificar temas; elaborar ‘machetes’ con información que se necesita retener; confeccionar y consultar carteles o afiches; rehacer en pequeños grupos pruebas; organizar tutorías entre alumnos/as para que ayuden a otros con los temas que más dominan, entre otras propuestas” (pp. 41-43).
Ejes de contenido
Números naturales
“Los alumnos/as han estudiado en primer ciclo cómo leer, escribir, ordenar números hasta aproximadamente 10000 ó 15000. En el segundo ciclo la comprensión de las reglas que subyacen a nuestro sistema de numeración, y la información sobre ‘números redondos’, permitirá que los alumnos/as puedan leer o escribir cualquier número natural. Del mismo modo, el incipiente análisis del valor posicional que han abordado en el primer ciclo, descomponiendo y componiendo con 10, 100 y 1000, en este ciclo les permitirá comprender la naturaleza más profunda de nuestro sistema: el agrupamiento en base 10 y la posicionalidad, de tal manera de aprender a ‘ver’ en la escritura del número la información que porta y la potencia para cálculos de suma, resta, multiplicación y división por la unidad seguida de ceros. Paralelamente, el estudio de diversos sistemas de numeración antiguos tiene el propósito, de favorecer la comparación entre sistemas para enriquecer y complejizar la mirada respecto del que se usa actualmente” (p. 145).
Operaciones con números naturales
“Al mismo tiempo que se trata de recuperar la diversidad de cálculos y problemas abordados en el primer ciclo, será necesario construir nuevos sentidos, especialmente para la multiplicación y la división. Harán su aparición nuevos problemas de división, tales como los que involucran la relación entre dividendo, divisor, cociente y resto, o los problemas en los que se repite una cantidad y es necesario determinar cuántas veces. Además de una ampliación de la clase de problemas, el estudio de estas operaciones abarcará también aspectos más ‘internos’ a su funcionamiento: la exploración y formulación de las propiedades, por ejemplo. Un nuevo aspecto, asociado a la multiplicación y a la división, serán las ideas de múltiplos, divisores y divisibilidad. Estas cuestiones se presentarán a partir de una diversidad de problemas, algunos con enunciados verbales y otros estrictamente numéricos que permitirán avanzar sobre ciertas prácticas de argumentación y demostración” (p. 145).
Números racionales
“Deberán explorar diversos tipos de problemas para los cuales las fracciones son un medio de solución, por ejemplo problemas de reparto y partición, problemas de medida, etc. Pero también - del mismo modo que para los números naturales - deberán enfrentarse a desentrañar algunas cuestiones de su funcionamiento, tales como la comparación, el orden, el cálculo, las diferentes maneras de representar una misma cantidad, etc. Respecto de las expresiones decimales también se propondrá una entrada a través de su uso social - el dinero y la medida – para luego adentrarse en cuestiones internas ligadas al valor posicional, al orden, al cálculo, a la búsqueda de un número entre dos dados, a la equivalencia con infinitas expresiones fraccionarias, etc El estudio de los números racionales enfrentará a los alumnos/as a algunas rupturas en relación con el trabajo en el campo de los números naturales. Por ejemplo, algunas relaciones que eran válidas para los números naturales (‘un número, si es más largo que otro, seguro es mayor’, ‘entre 2 y 3 no hay ningún número’, ‘si se multiplica, el número se agranda’), dejan de ser ciertas cuando aparecen los números racionales (ya que un número puede ser más largo que otro y ser menor - 1,9999 y 2 -, entre 2 y 3 habrá infinitos números y si se multiplica por 0,5 el número ‘se achicará’)” (pp. 145-146).
Proporcionalidad
“El punto de partida para su estudio nuevamente será el uso que los niños/as ya conocen de esta relación: sencillos problemas en los que se requiere multiplicar o dividir en torno a series proporcionales y poner en juego las ideas de dobles, mitades, triples, etc. Pero en este ciclo su estudio implicará un análisis más profundo de las propiedades de la proporcionalidad, de la constante, del porcentaje y también de los límites de esta noción para resolver problemas. Este contenido articula cuestiones ligadas a los números naturales y racionales, sus operaciones y conocimientos ligados al campo de la medida” (p. 146).
Geometría y espacio
“Figuras y cuerpos geométricos: través de problemas de construcción y de determinación de medidas – sin medir – y usando las propiedades estudiadas se favorecerá que los alumnos/as aprendan que los conocimientos son un medio para poder establecer afirmaciones sobre los objetos con los que tratan, sin necesidad de apelar a la constatación empírica. En el primer ciclo los niños/as validan sus producciones recurriendo a ejemplos, a constataciones empíricas y a argumentos muy ligados al contexto en que produjeron sus resultados. En el segundo ciclo resulta fundamental generar condiciones para que los alumnos/as comiencen a elaborar argumentos que validen sus afirmaciones apoyados en propiedades de las figuras. La validación empírica, será entonces insuficiente, por ejemplo no es posible demostrar que la suma de los ángulos interiores del triángulo mide 180º por medir y sumar sus ángulos, ya que si se miden, no dará justo 180º. Será necesario elaborar otras formas de justificación.
Espacio: propone retomar del primer ciclo los problemas de la representación plana. Interpretar planos que den cuenta de relaciones en el espacio físico y permitan anticipar decisiones es el objetivo prioritario propuesto para 4º y 5º años” (p. 146).
Medida
“Se propondrá a partir del uso social, de la exploración de algunas unidades de medida y de instrumentos usados fuera de la escuela que han circulado en el primer ciclo. En este ciclo se propondrá un análisis más riguroso de los múltiplos y submúltiplos de las unidades de medida de longitud, capacidad y peso. Por otro lado se iniciará a los alumnos/as en el estudio del perímetro y el área desde dos perspectivas. Una de ellas dirigida a la diferenciación de ambas nociones y a sus aspectos más cualitativos, y la otra - a fines del 2º ciclo - asociada a la determinación y cálculo de áreas y perímetros y el establecimiento de las unidades convencionales. El tratamiento del sistema de medidas será analizado a la luz de sus vinculaciones con el sistema de numeración decimal, la multiplicación y la división por la unidad seguida de ceros y las relaciones de proporcionalidad” (p. 146).
Qué se espera
“El segundo ciclo deberá asegurar que todos los alumnos/as realicen aprendizajes matemáticos consistentes sobre Números Naturales y sus Operaciones; Múltiplos, Divisores y Divisibilidad; Números Racionales y sus Operaciones; Circunferencias, Círculos, Triángulos y Cuadriláteros; Cuerpos Geométricos; Proporcionalidad; Sistemas de Medida; Área y Perímetro de algunas figuras. (…) nos parece importante señalar que una buena calidad de aprendizajes no implica ‘adelantar’ contenidos que no corresponden al segundo ciclo de la Educación Primaria. Por ejemplo, números enteros negativos, ecuaciones, probabilidad, estadística, potenciación y radicación, volumen, división entre fracciones, perímetro y área de polígonos y figuras circulares, figuras poligonales complejas, uso de llaves y corchetes, serán contenidos a tratar a partir de 1º ES. Evidentemente un docente que evalúe que sus alumnos/as logran disponer de todos los conocimientos propuestos para el 2º ciclo, puede aventurarse en la exploración de alguno de estos contenidos, aunque no sean requeridos para la promoción” (p. 147).
Diseño curricular para 1er año (7mo ESB), Pcia. de Buenos Aires Fuente: Diseño Curricular de Educación Secundaria 1er año_2006
1er año
Matemática.
Carga horaria: 4 Módulos semanales
Ejes
(campo de conocimiento)
Geometría y magnitudes
Núcleos de contenidos
Cuerpos. Figuras regulares. Lugar geométrico. Medida. Perímetro. Área. Volumen
Este eje exige un trabajo de descubrimiento y análisis de propiedades de figuras y cuerpos. Las construcciones que se proponen se relacionan con el uso de elementos de geometría, los lugares geométricos y la proporcionalidad.
En cuanto a la medida, se plantea un trabajo de reconocimiento de la importancia de cuestiones como la independencia área-perímetro y la equivalencia entre diferentes formas de expresión de medidas de magnitudes.
Número y operaciones
Operaciones con números naturales. Divisibilidad. Números racionales positivos
En este eje, se explicita la necesidad de trabajar con diferentes tipos de cálculo.
Se pretende que se incluyan estrategias para que la calculadora se aprenda a manejar con destreza, convirtiéndose en una herramienta al servicio del pensamiento en la búsqueda de respuestas.
Introducción al álgebra y al estudio de las Funciones
Lectura, interpretación y construcción de gráficos y tablas. Proporcionalidad. Introducción al trabajo
En este eje, se trabajará con el pasaje de la aritmética al álgebra, permitiendo generalizar propiedades de los números, expresar dependencia de variables en fórmulas y organizar información a través del lenguaje de las funciones.
Probabilidades y Estadística
Fenómenos y experimentos aleatorios. Estadística y probabilidad
Es posible que la probabilidad y la estadística sean un campo de trabajo nuevo para los/as alumnos/as, por esta razón, se pretende un estudio cualitativo de la probabilidad.
Se promueve la construcción de tablas estadísticas, la determinación de algunas medidas de tendencia central y el trazado y estudio de gráficas.
Expectativas de logro
Al finalizar el año, se espera que los/as alumnos/as:
Implementen diferentes modalidades de cálculo de acuerdo con las necesidades en el marco de la resolución de problemas.
Usen estratégicamente calculadoras en la resolución de problemas que requieran cálculos mecánicos y ajuste de estimaciones.
Utilicen lenguaje matemático en la comunicación tanto durante el desarrollo de las actividades como en la puesta en común de las producciones construidas.
Analicen, comparen y debatan sobre distintas soluciones de un problema y elijan la mejor, fundamentado la elección.
Construyan figuras como representación de entes geométricos descriptos o de situaciones geométricas y extrageométricas.
Usen en forma autónoma reglas, escuadras, compases, transportadores y, en caso de disponerse, de software geométrico para la construcción de figuras.
Reconozcan situaciones en las cuales sea adecuada la aplicación de la proporcionalidad.
Construyan tablas estadísticas que resuman información necesaria para la elaboración de hipótesis.
Construyan gráficos cartesianos y estadísticos.
Interpreten matemáticamente gráficos y tablas.
Ordenen cualitativamente sucesos de acuerdo con la probabilidad relativa de uno con respecto al otro.
Midan cantidades de distinta magnitud usando unidades convencionales.
Orientaciones para la evaluación
“La evaluación en esta materia deberá hacer ver a los
alumnos/as la importancia de superar la sola memorización. Como en las clases se prioriza la
participación y el hacerse cargo de la resolución de problemas matemáticos, esto
deberá tenerse en cuenta a la hora de evaluar (…) Los instrumentos de evaluación
que se utilizan en esta etapa no deben medir sólo el dominio de mecanismos o la
memorización de algoritmos, porque ese no es el sentido ni el enfoque de esta propuesta
curricular. La evaluación es un proceso que brinda insumos a docentes y alumnos/as para conocer
el estado de situación de la tarea que realizan juntos. (…) Es importante que la
calificación sea reflejo de la distancia entre lo que se espera que los alumnos/as logren y lo
efectivamente logrado por ellos. El alumno/a debe conocer claramente esto que se espera que logre
(…) La carpeta, además de incluir el registro de las actividades realizadas, debe contener
lo que se debe estudiar.
Finalmente, la comunicación y el intercambio logrados en cada clase
de matemática no deben interrumpirse por la aplicación de ningún instrumento de
evaluación” (p. 195).