Segregación residencial y tamaño de la ciudad en ciudades argentinas. ¿Una correlación real o ilusoria?

Residential segregation and city size in Argentine cities. A real or illusory correlation?

Consejo Nacional de Investigaciones Científicas y Técnicas. Centro de Estudios Urbanos y Regionales, Argentina.

Los estudios urbanos clásicos han encontrado una fuerte correlación estadística entre segregación residencial y tamaño de las ciudades. Sin embargo, también se ha sostenido que la correlación podría ser espuria, un efecto del Problema de la Unidad Espacial Modificable (PUEM). En este trabajo, nos proponemos avanzar en una demostración más concluyente sobre la cuestión. Encontramos que la correlación puede ser parcialmente espuria, pero no del todo ilusoria. La distribución del ingreso y otras formas de desigualdad pueden estar relacionadas con el tamaño de la ciudad, redundando por lo tanto en mayores niveles de segregación.

Classical urban studies have found a strong statistical correlation between residential segregation and city size. However, it has also been argued that this correlation could be spurious, a consequence of the Modifiable Areal Unit Problem (MAUP). In this study, we aim to provide more conclusive evidence on this issue. Our findings report that the correlation is partially spurious but not quite imaginary since income and other forms of inequality may be related to city size and hence have an impact on higher levels of segregation.

El estudio de la segregación residencial ha ocupado un lugar importante dentro de la sociología urbana desde los orígenes mismos de la disciplina a comienzos del siglo XX. Un sinfín de trabajos han sido conducidos con el afán de determinar en qué medida los individuos pertenecientes a diferentes grupos sociales se distribuyen desigualmente en el espacio urbano, cuáles son las causas y consecuencias de este fenómeno, y cuál es la mejor forma de medir la segregación a partir de indicadores de tipo estadístico que permitan conocer sus niveles actuales y su evolución a través del tiempo.

Las investigaciones producidas –en su inmensa mayoría anglosajonas– han mostrado sistemáticamente que existe una fuerte correlación estadística entre niveles de segregación y el tamaño de las ciudades, generalmente definido este último como la población total o el número de hogares que habitan una aglomeración urbana. En este sentido, los estudios empíricos han encontrado que las ciudades más pobladas tienden a estar más segregadas que las más pequeñas (Cowgill y Cowgill, 1951; Taeuber, 1964; Hwang et al., 1985; Telles, 1995; Wilkes y Iceland, 2004; Glaeser y Vigdor, 2006; Linares, 2013; Haque et al., 2018; Rodríguez, 2020).

La existencia de una correlación entre tamaño de la ciudad y segregación ha sido aceptada casi como una ley sociológica fundamental durante más de un siglo, hasta que fue desafiada en un sugerente e imprevisto trabajo de Douglas J. Krupka (2007). A partir de su estudio sobre ciudades de los EE.UU., el autor concluyó que todas las ciudades están igualmente segregadas y que cualquier regularidad empírica entre tamaño y segregación debe considerarse espuria, un simple artefacto estadístico, producto de cómo los organismos nacionales de estadística reúnen y divulgan la información censal, y de cómo, en consecuencia, ésta es utilizada por los investigadores. La ilusión estadística se relaciona con el conocido Problema de la Unidad de Espacial Modificable, o PUEM (Openshaw, 1984; Reardon y O ‘Sullivan, 2004; Velázquez, 2008), que se resume en que los índices de segregación son extremadamente sensibles a la escala espacial en que se recogen y publican los datos, y a restricciones sobre la cantidad aproximada de población que deben contener las unidades geoestadísticas. De esta manera, y dado que las ciudades más grandes son más densas (o asumiendo que lo son), la mayor densidad conlleva unidades espaciales de menor superficie, y esta menor superficie tiende a que las mismas sean más homogéneas en su interior y heterogéneas entre sí, de acuerdo con el principio básico de lo que en geografía se conoce como autocorrelación espacial (Celemín, 2009; Buzai y Montes Galbán, 2021)

En respuesta a los hallazgos de Krupka, un trabajo reciente realizado por Matias Garretón et. al. (2020) sobre ciudades chilenas pretende haber aportado nuevas evidencias que cuestionan la hipótesis de la correlación espuria. A partir del uso de índices de segregación que los autores consideran insesgados e inmunes a las inclemencias del PUEM, concluyen que las ciudades más grandes efectivamente son más segregadas.

Es nuestro entender que ambos trabajos –a pesar de llegar a conclusiones opuestas– comparten limitaciones metodológicas importantes que deben ser discutidas y resueltas. El propósito de este artículo es, entonces, revisitar la hipótesis de la correlación espuria (HCE) mediante la recopilación de nuevas evidencias y pruebas estadísticas adicionales, incluyendo variables espaciales específicas para controlar los efectos PUEM que no han sido empleadas en ningún estudio previo conocido: la superficie de la ciudad y de las unidades espaciales. Los índices de segregación residencial socioeconómica (SRS) se calculan para una muestra (sin precedentes) de 617 ciudades argentinas, utilizando datos del Censo 2010. Mediante el análisis de regresión, nuestro objetivo es determinar si el tamaño de la ciudad pierde parte o incluso todo su poder predictivo cuando se controlan los efectos del PUEM.

La segregación residencial suele definirse a grandes rasgos como la distribución desigual o separación de los grupos sociales en el espacio urbano (White, 1986; Massey y Denton, 1988). Dentro de un enfoque clásico –inspirado en la Ecología Humana de Chicago– se admite que cualquier grupo se considera segregado si está desigualmente distribuido en el espacio, independientemente de qué grupo se trate y de cómo se lo defina (Sabatini et al., 2001). Un enfoque alternativo, en cambio, entiende que no todo grupo desigualmente distribuido en el espacio es un grupo segregado. En este sentido, para hablar de segregación debemos estar en presencia de una distribución desigual que es la manifestación espacial de alguna forma de compulsión –económica o política, y no necesariamente intencional– ejercida por unos grupos sobre otros (Marcuse, 2001; Duhau, 2003; Rodríguez Merkel, 2014)

Más allá de la cuestión conceptual sobre si toda distribución desigual es o no segregación, lo relevante a los fines de este trabajo es que el grado en que diferentes grupos sociales se distribuyen desigualmente en el espacio puede aproximarse –y así ha sido a lo largo del último siglo– a través de fórmulas matemáticas que utilizan datos censales que cuentan con algún nivel de agregación espacial, como los llamados census tracts en EE. UU., o los radios censales en Argentina.^[1] Quizás por su facilidad de cálculo e intuitiva interpretación, el más conocido y popular es el llamado Índice de Disimilitud D (Duncan y Duncan, 1955); D varía de 0 a 1 y se interpreta como la proporción de cada grupo (dada una clasificación dicotómica) que tendría que cambiar su zona de residencia para distribuirse equitativamente en todas las zonas de la ciudad. Sin embargo, existen decenas de índices de segregación adicionales propuestos en la literatura que abordan diferentes dimensiones del fenómeno (Massey y Denton, 1988) y cuyas ventajas y limitaciones han sido extensamente documentadas en diversos trabajos (White, 1983, 1986; James y Taeuber, 1985; Reardon y O' Sullivan, 2004; Marcos y Mera, 2011; Linares, 2013).

Cabe señalar que a partir del desarrollo y difusión que han alcanzado los sistemas de información geográfica (SIG) en las últimas décadas, ha sido posible proponer ajustes a muchos de los índices tradicionales, procurando recuperar cierta espacialidad ausente en los índices clásicos, principalmente en términos de cómo se disponen las unidades geoestadísticas en el espacio geográfico de la ciudad (White, 1986; Morrill, 1991; Wong, 1993; Dawkins, 2006; Rey y Smith, 2012; Crespo y Hernández, 2020). En teoría, la ventaja de los índices “espaciales” es que aportan una solución al problema conocido como el “tablero de ajedrez” (o checkerboard problem). Esto significa que no sólo consideran la distribución desigual de los grupos a través de unidades espaciales mínimas, sino también la medida en que estas unidades espaciales se distribuyen en forma aleatoria, dispersa o en clusters (agrupamientos) a diversa escala geográfica (Reardon y O' Sullivan, 2004; Fossett, 2017).

Ahora bien, con respecto a las explicaciones más comunes para la correlación entre segregación y tamaño de la ciudad (en términos poblacionales), las mismas se remontan a los orígenes de la propia sociología urbana. Retomando postulados previos de Émile Durkheim, Louis Wirth (1938) creía en cierto determinismo mecánico entre el tamaño de las concentraciones humanas, interacciones sociales entre grupos y niveles de diferenciación social, y de allí a diferentes clases de segregación: económica, racial, étnica, ocupacional, sexual, etaria, gustos, modos de vida, etc. Consistentemente con esta tesis de que la diferenciación social se refleja en diferenciación espacial, varios estudios posteriores han encontrado una fuerte correlación entre el tamaño de la ciudad y la desigualdad de ingresos (Betz, 1972; Long et al., 1977; Haworth et al., 1978; Nord, 1980; Baum-Snow y Pavan, 2013). Asimismo, se han reportado evidencias de una correlación positiva entre desigualdad económica y segregación a través de varios estudios en ciudades de Estados Unidos, China y Argentina (Watson, 2009; Reardon y Bischoff, 2011; Florida y Mellander, 2018; Rodríguez, 2020; Shen y Xiao, 2020). En resumen, si las ciudades más grandes son más desiguales, esto ayudaría a explicar por qué están más segregadas.

A su vez, se han propuesto otras explicaciones adicionales para la correlación entre el tamaño de la ciudad y segregación. Una es que las ciudades más grandes simplemente tienden a ser más antiguas y, por lo tanto, reflejan los patrones residenciales más segregados de una época anterior (Farley y Frey, 1994; Logan et al., 2004; Glaeser y Vigdor, 2006). Otra, es que la mayor densidad poblacional de las grandes urbes aumentaría el deseo de los individuos de separarse de los miembros de otros grupos y que las más grandes tienen más espacio disponible para lograrlo (Glaeser y Vigdor, 2006). Sin embargo, y aunque existen evidencias de preferencias residenciales basadas en la raza (Boustan, 2011), atribuir esto al tamaño de la ciudad o a densidades más altas plantea algunas dudas. En primer lugar, no hay ninguna razón evidente por la que la densidad debería afectar el deseo de los grupos de separarse. Por otro lado, la idea de más espacio puede tener varios significados. Si se refiere a más suelo disponible por hogar, esto sugiere que las ciudades más grandes son menos densas que las más pequeñas, lo que contradice la suposición anterior de que las más grandes son más densas. Más espacio también puede referir a la cantidad absoluta (no relativa) de suelo urbanizado; pero incluso en este caso, no está claro por qué dos o más grupos no pueden separarse perfectamente, independientemente de la cantidad total de suelo disponible.

El planteo inicial de la HCE fue desarrollado por Krupka en su artículo de 2007, ¿Are big cities more segregated? Neighborhood scale and the measure of segregation, donde el autor propuso su controvertida hipótesis de que a pesar de cierto imaginario que percibe a las ciudades más pequeñas de EE. UU. como más igualitarias, en realidad podrían ser tan segregadas como las ciudades más grandes. Según Krupka, el carácter espurio de la correlación entre el tamaño de la ciudad y la segregación tiene su origen en cierta inconsistencia o incompatibilidad de los criterios que se aplican a la delimitación de las unidades espaciales que se utilizan para divulgar y procesar la información censal. En los EE. UU., se da el caso de que rige un doble criterio para delimitar los llamados census tracts. Por un lado, su traza debe procurar corresponder a vecindarios reales en el territorio, homogéneos en su composición socioeconómica y étnico/racial (lo que no impone, a priori, ningún límite a su tamaño). Por otro lado, sin embargo, la delimitación de los census tracts debe contemplar una restricción de población (population constraint) que dicta que deben contener aproximadamente 4000 habitantes.^[2] Al respecto, Krupka (2007) considera que el segundo criterio termina generalmente imponiéndose al primero, resultando en dos cuestiones que hacen al carácter espurio de la correlación. Por un lado, en que "el vecindario, sea lo que sea, no está representado en los datos censales utilizados para medir y comparar la segregación entre ciudades" (p. 177). Por otro lado, en que, si las ciudades más grandes son más densas tendrán entonces unidades espaciales más pequeñas en superficie; y estas unidades, cuanto más pequeñas en superficie, tenderán a ser más homogéneas en su interior y más diversas entre sí.^[3] De esta manera, la restricción de población de 4000 habitantes (podría ser cualquier otra, no importa, siempre y cuando sea la misma en todas las ciudades) lleva a la falsa ilusión de que las ciudades más pequeñas tengan niveles de segregación más bajos, simplemente porque –al ser menos densas– sus vecindarios pequeños y segregados no tienen suficiente población para llenar un census tract, y se ven agrupados todos en una misma unidad geoestadística vecindarios contiguos pero muy disímiles.

Para contrastar su hipótesis, Krupka realizó algunas pruebas estadísticas basadas en datos del censo de EE. UU. del año 2000, correspondientes a una muestra de 265 ciudades, o Áreas Estándar Metropolitanas (MSA, por sus siglas en inglés). Para cada MSA, calculó el Índice de Disimilitud (para segregación racial, con los individuos como unidad de análisis) y el índice de Jargowski (para segregación económica, medida por ingresos, con hogares como unidad de análisis).

Como primera prueba, Krupka calculó una correlación bivariada simple entre el tamaño de la ciudad (cantidad habitantes y hogares) y los niveles de segregación (racial y económica) en cuatro niveles de agregación espacial decreciente (condado,^[4] zona postal,^[5] census tract^[6] y bloque censal^[7]). Según Krupka (2007), si la correlación es espuria, los coeficientes deberían disminuir a medida que la escala de agregación espacial disminuye. Tal expectativa se basa en que “a medida que las unidades espaciales se hacen más pequeñas, es menos probable que vecindarios disímiles se agrupen falsamente en la misma unidad espacial” (p. 190). Los resultados parecen darle la razón, pues muestran una disminución casi monótona en las puntuaciones de correlación (véase Tabla 1). No obstante, Krupka nota una anomalía al pasar de condados a zonas postales usando el índice de Jargowski para hogares, aunque no la considera suficiente para refutar su hipótesis, pues si bien las zonas postales son en promedio más grandes que los census tracts, no son estrictamente agrupamientos de estos.

Tabla 1. Correlación entre segregación y tamaño de la ciudad para cuatro escalas de agregación espacial

Fuente: Adaptado de Krupka (2007). Nota: D y J son, respectivamente, el Índice de Disimilitud de Duncan (para segregación racial) y el Índice de Clasificación de Vecindarios de Jargowski (para segregación económica). Se correlacionan con el valor absoluto de población y hogares en su transformación logarítmica. Todos los coeficientes son significativos al 0,05. N = 265.

En una segunda prueba (véase Tabla 2) Krupka realiza un análisis de regresión sobre las puntuaciones de segregación racial con sólo dos variables independientes: la población total y el número de unidades espaciales en que se divide la ciudad. Ahora, espera que:

Si el tamaño [de la ciudad] es la causa de patrones residenciales más segregados, entonces la población debería correlacionarse con niveles más altos de segregación, incluso cuando mantenemos constante el número de vecindarios ... Por otro lado, si la correlación entre la escala urbana y segregación es un artefacto del proceso de recolección de datos, el efecto del tamaño de la población debería ser insignificante, y el número de barrios debería ser el principal determinante de la segregación. (Krupka, 2007, p. 191)

Una vez más, Krupka afirma haber encontrado evidencias consistentes con la HCE. Por un lado, agregar población a un número constante de unidades espaciales no tiene un efecto positivo sobre la segregación; de hecho, el efecto es mayormente negativo, excepto a nivel de condado. Por otro lado, cuando el tamaño de la población se mantiene constante, el coeficiente del número de unidades espaciales es positivo, y tiende a hacerse más fuerte cuanto menor es la agregación espacial.

Sin pretensiones de invalidar el trabajo de Krupka (por demás inspirador) creemos que sus pruebas distan de ser concluyentes. El motivo es sencillo, y es que no ha incluido la densidad ni la superficie de las unidades espaciales como variables predictoras de la segregación. El autor simplemente da por sentado que las ciudades más pobladas son más densas, y que la densidad naturalmente aumentará al agregar población sobre un número constante de unidades espaciales. Pero esto no tiene por qué ser así. En las regresiones, el coeficiente negativo del tamaño de la población bien puede ser el efecto de que la superficie de las unidades espaciales (y de la ciudad) también se incrementa al sumarle habitantes, lo que explicaría, entonces, los menores niveles de segregación ya que las unidades espaciales –al aumentar su tamaño– tienden a volverse más heterogéneas en su interior.

La HCE también fue abordada en un estudio más reciente de Garretón et al. (2020), a partir del cual los autores obtuvieron resultados opuestos a los de Krupka. Utilizando una muestra de 98 ciudades chilenas, también realizaron un análisis de regresión sobre los niveles de segregación, con la población total y número de unidades espaciales como variables explicativas o predictores.

La diferencia sustancial con el trabajo de Krupka es que los autores recurrieron al uso de una variante del índice de Jargowski (J) a la que consideran insesgada espacialmente (spatially unbiased). Básicamente, se trata de calcular un índice J a partir de datos aleatorios, y restar este valor al índice J absoluto o real. Según los autores, “por definición, el nivel de segregación medido con datos aleatorios es un efecto espurio, por lo que descontamos estos valores de las mediciones con datos reales, obteniendo así medidas de segregación espacialmente no sesgadas a múltiples escalas” (Garretón et al., 2020, p. 8). El resultado de este procedimiento fueron dos nuevos índices:

primero, el índice de Jargowski diferencial, definido como la diferencia máxima entre los valores reales y aleatorios, que también define la escala de segregación más fuerte; y, en segundo lugar, el índice de Jargowsky integral, calculado como un promedio de los índices de Jargowsky diferenciales obtenidos para todos los niveles de agregación. (Garretón et al., 2020, p. 9)

Los resultados reportados por Garretón y sus colegas desafían las conclusiones de Krupka, en el sentido de que sí parece haber un efecto positivo, significativo y no espurio del tamaño de la ciudad sobre la segregación económica (Tabla 3). Indistintamente de que se utilice el índice J Integral o Diferencial, esta vez la segregación no desciende, sino que aumenta al agregar población sobre un número constante de unidades espaciales. Según explican los autores, los “mayores índices de segregación probablemente se deban a varios procesos que afectan a las principales metrópolis chilenas, como la concentración de trabajadores altamente calificados, el rápido aumento del valor del suelo, los desarrollos masivos de viviendas y la gentrificación” (Garretón et al., 2020, p. 12). Curiosamente, no mencionan las desigualdades socioeconómicas como factores que pudieran incidir en mayores niveles de segregación, pero eso es un tema que excede lo estrictamente metodológico que abordamos en este trabajo.

Tabla 3. Regresiones sobre la segregación económica medida por índices supuestamente insesgados

El trabajo de Garretón y sus colegas también amerita al menos dos objeciones metodológicas importantes. Por un lado, los autores basan todas sus conclusiones sólo en la observación de lo que sucede con el tamaño de la población como variable predictora. No así con la variable cantidad de unidades espaciales, la cual se comporta de manera curiosa y contraintuitiva: al agregar unidades espaciales sobre una población de tamaño constante, la segregación disminuye en vez de aumentar. Los autores toman nota de esta anomalía, pero le restan importancia, limitándose a señalar que los coeficientes de regresión “no son significativos” (Garretón et al., 2020, p. 12). Tal afirmación es visiblemente errónea, pues la propia tabla muestra que los coeficientes, para esta variable, también tienen valor p de 0,000.

Por otro lado, si bien es cierto que el uso de índices de segregación ajustados por alguna segregación esperada basada en datos aleatorios ha sido propuesto hace décadas (Cortese et al., 1976; Winship, 1977), este recurso nunca estuvo pensado para obtener índices de segregación espacialmente insesgados, tal como sostienen los autores. De hecho, no existe ninguna razón evidente por la que los índices J Integral y Diferencial –ni cualquier otro conocido– deberían tener algún control sobre los efectos del PUEM. Los autores no brindan ninguna fundamentación al respecto, por lo que no resulta posible debatir semejante afirmación en términos formales. Aun así, mostraremos a través de un sencillo ejemplo cómo los índices de segregación ajustados por segregación aleatoria no son espacialmente insesgados, y siguen siendo sensibles al tamaño de la población cuando se aplican restricciones en cuanto al número de individuos que deben contener las unidades espaciales censales (véase Figura 1).

Imaginemos dos ciudades con su población distribuida en partes iguales entre dos grupos sociales A y B (una proporción de 50 y 50) y con idénticos patrones de segregación. En el ejemplo, ambas ciudades tienen 64 manzanas, pero la ciudad más pequeña tiene una población de 6.400 habitantes, mientras que la ciudad más grande es más densa pues tiene una población de 12.800. En cada manzana, el número superior indica los individuos del grupo A, y los individuos del grupo B están representados por el número debajo. La escala de grises ilustra la concentración relativa del grupo A (sombreado más oscuro) y el grupo B (sombreado más claro), lo que nos ayuda visualizar un evidente patrón de segregación.

Aquí debemos adoptar un supuesto importante: que todos estaríamos de acuerdo en que ambas ciudades están igualmente segregadas. Esto es más que simple intuición, pues, de hecho, si calculamos las puntuaciones de segregación a nivel de manzana, son las mismas en ambas ciudades (índice de segregación de Gini = 0,63^[8]). Así, gracias a que los datos están disponibles al mismo nivel de agregación espacial y sin restricción de población, el índice de segregación efectivamente las muestra como igual de segregadas.

Figura 1. Puntuaciones de segregación para ciudades con tamaños distintos, sin restricciones de población. Distribución simulada a nivel de manzana

Sin embargo, supongamos que no disponemos de estos datos a nivel de manzana porque existe una restricción estricta de 400 habitantes por zona censal. Como consecuencia, ambas ciudades necesariamente diferirán en el número de unidades espaciales que contienen: la ciudad más pequeña tendrá 16 zonas censales y la ciudad más grande 32 (Figura 2). Ahora sí, la ciudad más grande aparecerá como falsamente más segregada que la más pequeña (0,60 frente a 0,58). Aquí es donde surge el PUEM, y continúa existiendo en las subsiguientes escalas de agregación espacial (Figura 3).

Figura 2. Puntuaciones de segregación para ciudades de diferentes tamaños, con una restricción de población de 400 por unidad espacial

Figura 3. Puntuaciones de segregación para ciudades de diferentes tamaños, con una restricción de población de 800 por unidad espacial

Examinemos, pues, si los índices ajustados a partir de datos aleatorios permiten obtener medidas espacialmente insesgadas, tal como afirman Garretón y sus colegas. En la Tabla 4 se muestran los puntajes de segregación de Gini (real, integral y diferencial)^[9] para ambas ciudades a niveles crecientes de agregación espacial. Si los índices calculados a partir de datos aleatorios tuvieran algún control sobre el PUEM, entonces esperaríamos que los índices de Gini diferencial e integral fueran idénticos en ambas ciudades en cada nivel de restricción de población, es decir, mostrándolas igualmente segregadas a todas las escalas. Cabe aquí aclarar que utilizamos el índice de Gini y no el de Jargowski, ya que nuestra variable de segmentación es dicotómica, mientras que el índice J requiere de información para una variable cuantitativa (como ingresos). No obstante, el uso de uno u otro índice no debería marcar ninguna diferencia, siempre y cuando se aplique el mismo procedimiento de ajuste por datos aleatorios. La fórmula de Gini es como sigue:

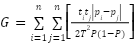
donde ti y pi son la población absoluta y proporción del grupo en la i-ésima unidad espacial; T y P son la población absoluta y la proporción del grupo en la ciudad en su conjunto, que se subdivide en n unidades espaciales.

Tabla 4. Puntuaciones de segregación reales y ajustadas por datos aleatorios para ciudades de diferentes tamaños, con niveles crecientes de restricción poblacional

Los resultados de la simulación muestran que, en todas las escalas, la ciudad más grande tiene una puntuación de segregación aleatoria más alta, y que disminuye a medida que aumenta la escala de agregación. Esto no debería sorprendernos ya que, cuantas menos subdivisiones tengamos, más se aproximará una distribución aleatoria a una distribución perfecta de 50-50.

Con respecto al índice de Gini diferencial, la simulación muestra que la ciudad más pequeña y la más grande no solo puntúan de manera diferente, sino que también alcanzan su puntaje máximo en diferentes niveles de restricción poblacional. Mientras que la ciudad más pequeña alcanza la diferencia máxima en 400 individuos por zona (0,525), la ciudad más grande la alcanza en una población de 200 por zona (0,548). Ergo, no son comparables.

Veamos ahora el índice de Gini Integral. Por cierto, este índice no es fácil de establecer, pues los autores no brindan mayores detalles. ¿Cuáles son las puntuaciones que debemos promediar? La solución más inteligente parecería ser la de promediar sólo aquellas puntuaciones correspondientes a escalas para las que disponemos de datos reales (dada la restricción de población impuesta en los datos). Siguiendo este razonamiento, la mejor opción sería la B, donde se promedian las escalas de agregación 2, 4, 8 y 16 para la ciudad más pequeña, y las escalas 2, 4, 8, 16 y 32 para la ciudad más grande. Y aunque las opciones A, C y D también podrían tener sentido, la cuestión resulta irrelevante: cualquiera sea el rango de valores que promediemos, la ciudad más grande siempre está significativamente por encima de la ciudad más pequeña.

A partir de esta simulación, podemos concluir que los índices de segregación ajustados por datos aleatorios no son espacialmente insesgados. Fallan en identificar como igualmente segregadas dos ciudades de diferente tamaño, pero con idénticos patrones de segregación. En definitiva, el problema del trabajo de Garretón es que tampoco introduce superficies y densidades en el análisis de regresión.

Entonces, ¿las ciudades más grandes tienden a ser más segregadas, o es solo una ilusión estadística? A diferencia de los trabajos de Krupka y Garretón et al., aquí creemos que cualquier intento de responder esta pregunta debe considerar no sólo la población total y el número de unidades espaciales sino también la densidad y la superficie de la ciudad (y de las unidades espaciales) como variables relevantes en el análisis estadístico. En otras palabras, es preciso tratar de controlar las puntuaciones reales de segregación por variables proxy de los efectos del PUEM.

Por otro lado, la HCE debe formularse de una manera simple e intuitiva, sin depender de un concepto vago y ambiguo como el de vecindario al que apela Krupka. Si las zonas censales delimitasen perfectamente zonas residenciales homogéneas desde el punto de vista económico o racial –como propone Krupka– las puntuaciones de segregación siempre serán iguales a 1 (segregación máxima). No habría forma de someter a prueba la HCE en tal escenario.

Nuestra formulación de la HCE supone que: 1) los grupos raciales o económicos tienden a estar distribuidos de manera desigual en el espacio residencial; 2) las ciudades más grandes son más densas; y 3) se ha utilizado una restricción poblacional al trazar las zonas censales que agrupan los datos de población; de allí, 4) densidades más altas harán que las ciudades más grandes tengan unidades espaciales de menor superficie; y 5) las unidades espaciales de menor superficie tenderán a ser más homogéneas. El resultado será que las urbes más grandes mostrarán puntuaciones de segregación más altas que las más pequeñas, incluso si todas tuviesen el mismo patrón de segregación (recuérdese las Figuras 2 y 3).

Bajo estos supuestos, podemos pensar en dos posibles formas de testear la HCE sin ninguna incidencia del PUEM. Una sería acceder a microdatos de individuos u hogares completamente desagregados espacialmente –cada uno georreferenciado a coordenadas de latitud y longitud precisas– y posteriormente, agrupar estos microdatos en unidades espaciales de idéntica forma y tamaño, preferentemente una malla hexagonal colocada aleatoriamente sobre los datos espacializados (Rodríguez, 2013). Hecho esto, procederíamos a calcular cualquier índice de segregación que elijamos y ejecutar un análisis de correlación simple entre tamaño de la ciudad y segregación en una muestra de ciudades suficientemente grande. Sin embargo, como sabemos, esta opción no está disponible para los investigadores en este momento, debido a cuestiones de confidencialidad de los datos y resguardo del llamado secreto estadístico.

Una segunda opción, más viable y sencilla, para abordar la HCE es la que proponemos en este documento: calcular las puntuaciones de segregación para todas las ciudades, y someterlas a un análisis de regresión frente a un conjunto de variables independientes, incluidas densidad y superficie (de la ciudad y, especialmente, la superficie media de las unidades espaciales). Téngase en cuenta que no se trata aquí de construir índices espacialmente insesgados, sino de determinar el carácter espurio o no de la correlación.

La variable dependiente por explicar es la segregación residencial socioeconómica (SRS) la cual definimos operacionalmente como la distribución desigual de dos grupos socioeconómicos, definidos estos, a su vez, por el máximo nivel educativo de los jefes y jefas de hogar: un grupo de nivel socioeconómico bajo (hogares con jefes y jefas sin educación y hasta secundaria incompleta)^[10] y uno de nivel socioeconómico alto (jefes y jefas con secundaria completa o más). El nivel educativo de la persona que ocupa la jefatura del hogar evidentemente no agota la complejidad del concepto de nivel socioeconómico, pero puede considerarse una buena aproximación empírica al mismo, especialmente en países donde los censos no relevan información sobre ingresos. Por lo demás, y aunque no se trata aquí de un estudio longitudinal, esta variable es la única que –en Argentina– se ha relevado y resulta comparable a lo largo de todos los censos desde, por lo menos, 1960.

Siguiendo las recomendaciones de Michael White (1986), optamos por utilizar el Índice de Gini (G) en lugar del Índice de Disimilitud de Duncan para medir la segregación. Gini también varía de 0 a 1, pero a diferencia de D y otros índices como el de Entropía (H), “el índice de Gini satisface los cuatro criterios de calidad” (p. 204). El índice de Gini se calculó sobre una muestra grande (de hecho, casi todo el universo) de 617 aglomeraciones con al menos 5 radios censales urbanos. Los microdatos a nivel de radio censal pertenecen al censo nacional argentino de 2010.^[11]

Para este trabajo no hemos considerado utilizar índices de tipo “espaciales”, ya que su cálculo para un número tan grande de ciudades se vuelve extremadamente complejo por cuanto requiere generar rutinas específicas en SIG que, según el índice, computen relaciones de contigüidad y/o proximidad entre radios censales. Por lo demás, tampoco existe certeza sobre si el uso de un Gini “espacial” podría generar resultados significativamente distintos. Al respecto, según se desprende del trabajo de Casey Dawkins (2006), la correlación entre ambas versiones de Gini es significativamente alta (r=0,824 para 237 ciudades de los EE.UU.).

Se trabajó con las siguientes variables independientes, todas transformadas a su logaritmo con el fin de aproximar una distribución lineal de los puntajes y que los coeficientes no se vean afectados por valores extremos:

Muchas otras variables podrían incluirse en este análisis (edad de la ciudad, perfil económico, región, así como otros atributos geográficos, culturales o sociales). Sin embargo, nuestra principal preocupación no abarca todo el espectro de causas determinantes complejas de la segregación. Con el fin de llegar a una validación completa del HCE, esperamos encontrar los siguientes resultados:

• El tamaño de la ciudad estará positiva y significativamente correlacionado con la densidad, y lo mismo la densidad con la superficie media de los radios censales.

• En el análisis de regresión, la densidad debe ser un fuerte predictor de la superficie media de los radios censales.

• El tamaño de la ciudad (hogares) debería predecir positiva y significativamente la segregación cuando se controla por la superficie de la ciudad. Los coeficientes deben dejar de ser significativos cuando se controlan los efectos del PUEM (superficie media de las unidades espaciales). En su lugar, el número de unidades espaciales debe asumir todo el poder predictivo.

La Tabla 5 muestra la esperada correlación positiva y significativa entre SRS y tamaño de la ciudad (r=0,728). En Argentina, las ciudades más pobladas tienden claramente a aparecer como más segregadas. También existe una correlación casi perfecta entre la densidad poblacional de la ciudad y el tamaño de las unidades espaciales (r=0,879). Sin embargo, debemos notar que la correlación entre el tamaño de la ciudad y densidad poblacional no es muy importante (apenas r=0,358). Menos importantes aún (pero todavía significativas) son las correlaciones entre segregación y densidad poblacional de la ciudad (r=0,158), y entre segregación y superficie media de las unidades espaciales (r=0,123). Estos primeros resultados ya parecen poco consistentes con la HCE, especialmente porque ponen en duda el supuesto básico de que las ciudades más grandes son más densas.

Fuente: Elaboración propia. Nota: N = 617. Todas las correlaciones son significativas al nivel de 0,01.

El análisis de regresión presentado en la Tabla 2 debería ayudarnos a profundizar en el examen de la HCE. El modelo A1 confirma que la densidad poblacional es un muy buen predictor de la superficie media de las unidades espaciales (-0,774). El modelo B1 muestra las puntuaciones de segregación predichas por el tamaño de la ciudad y el número de unidades espaciales. Esta es una de las pruebas de Krupka, y los resultados tienen similitudes y diferencias: agregar población sobre una cantidad de unidades constantes aumenta la segregación; pero, en este caso, el tamaño de la ciudad (todavía definido como cantidad de hogares) tiene un coeficiente positivo, y no negativo (lo que resultaría, incluso, más consistente con la HCE que los datos de Krupka). Esta prueba, sin embargo, es de poco interés ya que, como hemos adelantado, no incluye la superficie de la ciudad y de las unidades espaciales como control.

Tabla 6. Regresiones sobre la superficie media de las unidades espaciales y puntuaciones de segregación

Las especificaciones B2, B3 y B4 deberían, ahora sí, permitir contrastar la HCE de forma más eficiente. En B2, la adición de hogares a una ciudad manteniendo constante su superficie (densificación) predice un aumento significativo de la segregación (0,052), lo que sí parece consistente con la HCE. Sin embargo, para una validación completa de la hipótesis, esperaríamos que este poder predictivo del tamaño de la ciudad se diluya cuando el número de unidades espaciales (B3) o la superficie media de las unidades espaciales (B4) se incluyen como controles. Al hacerlo, vemos que el coeficiente para el tamaño de la ciudad cae a menos de la mitad de su valor anterior (0,024), pero no desaparece. Esto sugiere que cerca de la mitad de la correlación entre segregación y tamaño de la ciudad es efectivamente espuria, pero que la mitad restante no lo es. Adicionalmente, cabe señalar que la cantidad y superficie media de las unidades espaciales^[12] tienen ambas un efecto significativo sobre la segregación en la dirección esperada, independientemente del tamaño de la ciudad.

Es interesante notar que la superficie total de la ciudad también explica la segregación bajo todas las especificaciones (a mayor superficie, mayor segregación), incluso cuando el total de hogares se mantiene constante. Así, el hecho de que ambas variables estén altamente correlacionadas (r=0,862) y aun así puedan explicar la segregación independientemente una de otra nos hace preguntarnos qué pasaría si redefiniéramos operativamente el tamaño de la ciudad como una combinación de la superficie de la ciudad y cantidad de hogares, en vez de sólo considerar la cantidad de hogares (véase Figura 4). Podemos probar la HCE bajo este enfoque alternativo simplemente controlando la superficie de la ciudad por su densidad. De esta manera, cualquier aumento en la superficie de la ciudad puede interpretarse como un aumento simultáneo y proporcional en la cantidad de hogares.^[13]

Las especificaciones C1, C2 y C3 son similares a B2, B3 y B4, pero donde el total de hogares se sustituye por densidad de la ciudad. C1 muestra que un crecimiento simultáneo en la superficie de la ciudad y los hogares tiene un importante efecto positivo en la segregación. Siguiendo el mismo razonamiento de B, ahora esperaríamos que el poder predictivo del tamaño de la ciudad se desvanezca –o al menos se debilite– cuando se controle la incidencia del PUEM. Manteniendo fijo el número de unidades espaciales (C2), vemos que ambos coeficientes para el tamaño de la ciudad (hogares y superficie) disminuyen sustancialmente, aunque esto puede ser consecuencia de que el aumento de la segregación se contrarresta con el aumento de la superficie y diversidad interior de las unidades espaciales (pues si la superficie de la ciudad aumenta, las unidades espaciales deben ser más grandes en superficie si su número es constante).

Los efectos del PUEM deberían controlarse de manera más efectiva en C3, donde el número de unidades espaciales se extrae del modelo y se reemplaza por la superficie media de las unidades espaciales. Los resultados son bastante sorprendentes: el tamaño de la ciudad no pierde nada de su poder predictivo; más aún, su coeficiente aumenta ligeramente de 0,074 a 0,076. Esto significa que un aumento del 1% en el tamaño de la ciudad se asocia, en promedio, con un aumento de 0,076 en los puntajes de segregación. En comparación con los resultados anteriores (las especificaciones B) estos nuevos hallazgos sugieren que la correlación entre tamaño de la ciudad y segregación es completamente genuina.

En esta investigación hemos intentado explorar la hipótesis de la correlación espuria (HCE) entre la segregación y el tamaño de la ciudad, previamente examinada por Krupka (sobre ciudades de EE. UU.) y Garretón et al. (sobre ciudades chilenas). Al incluir variables de área y densidad –ausentes en aquellos estudios– pudimos reunir evidencias más concluyentes con respecto a la HCE.

Las ciudades argentinas muestran una alta correlación entre segregación y tamaño de la ciudad. Basándonos en la suposición común de que las ciudades más grandes son más densas y, por lo tanto, tienen unidades espaciales censales más pequeñas –lo que hace que las puntuaciones de segregación sean más altas–, estábamos bastante seguros de que encontraríamos pruebas convincentes de que efectivamente se trataría de una correlación espuria. Los resultados, sin embargo, brindan poco o ningún sustento a esta hipótesis.

En primer lugar, las correlaciones entre el tamaño de la ciudad (medido como el total de hogares), la densidad y el tamaño de las unidades espaciales, son estadísticamente significativas, pero no tan grandes como se esperaría.

En segundo lugar, se llevó adelante un examen más profundo de la HCE a través de un análisis de regresión, donde el tamaño de la ciudad se definió primero como el total de hogares habitando en ciudades (o lo que en Argentina se define como localidades urbanas). La evidencia encontrada sugiere que la correlación entre el tamaño de la ciudad y la segregación no es completamente espuria: al introducir el número y superficie media de las unidades espaciales como controles, el poder predictivo del tamaño de la ciudad sobre la segregación disminuye, pero sigue siendo significativo. Es decir, la mayor segregación socioeconómica en ciudades más grandes puede no ser del todo ilusoria.

También examinamos la HCE bajo una definición operativa alternativa del tamaño de la ciudad: como una combinación del total de hogares y la superficie de la ciudad. Para ello, se realizaron regresiones adicionales con la superficie de la ciudad como predictora de la segregación, y la densidad manteniéndose constante. Los resultados mostraron en primer lugar que cuando la superficie de la ciudad y el total de hogares crecen simultánea y proporcionalmente, hay un gran aumento de la segregación. Un segundo e inesperado hallazgo es que el poder predictivo del tamaño de la ciudad permanece intacto cuando se agrega la superficie de las unidades espaciales como control. Este segundo conjunto de regresiones, ejecutadas bajo la definición alternativa de tamaño de ciudad, no es en absoluto compatible con la HCE; en cambio, los resultados sugieren que toda correlación entre la segregación socioeconómica y el tamaño de la ciudad puede ser completamente genuina.

Los hallazgos de este estudio pueden interpretarse como consistentes con la idea de que las grandes y pequeñas ciudades están lejos de estar igualmente segregadas, al menos en Argentina y bajo la metodología específica utilizada aquí. En suma, parece haber algo relacionado con el tamaño de la ciudad que hace que los grupos de menor nivel socioeconómico estén más segregados en urbes más grandes. Algunas posibles causas se han esbozado en la sección 2: las ciudades más grandes tienden a ser más diversas, desarrollan sistemas de estratificación y división del trabajo más avanzados y, al final, tienden a ser más desiguales en términos socioeconómicos, lo que maximiza la posibilidad de que los grupos de ingresos más altos segreguen a los grupos de ingresos más bajos.

Por supuesto, hay muchas otras variables –no todas las cuales admiten ser trabajadas a partir de datos censales– que también pueden variar según el tamaño de la ciudad, produciendo un efecto genuino en la segregación. Por ejemplo, la escala de los mercados inmobiliarios (las urbanizaciones cerradas y otros emprendimientos residenciales orientados a grupos de alto poder adquisitivo pueden ser rentables sólo en áreas urbanas más allá de cierto tamaño), las prácticas de planificación urbana, las políticas de vivienda, la edad de las ciudades o incluso las actitudes psicológicas y culturales de las poblaciones en diferentes regiones dentro de un mismo país.

Una mención especial merece el hecho de que, si bien no existen hoy en día índices de segregación insesgados e inmunes al PUEM, esto no es un problema intrínseco a las fórmulas matemáticas con que se calculan los índices, sino de la forma espacialmente agregada con que los investigadores podemos acceder a los mismos. Sin embargo, quienes sí disponen de microdatos sin agregación espacial, y de allí, todo lo necesario para calcular índices de segregación completamente insesgados, son los propios organismos nacionales de estadística.

Al respecto, es preciso recordar que la última Cumbre Hábitat III celebrada en Quito, Ecuador, elevó por primera vez la segregación residencial al rango de problema que afecta el Derecho a la Ciudad, y que debe ser contemplado por las políticas públicas en el marco de la Nueva Agenda Urbana (ONU, 2016). Más allá del carácter en buena medida declamativo que suelen tener esta clase de eventos internacionales ¿sería utópico pensar que los organismos de estadística –así como consideran importante medir indicadores de pobreza, desocupación o distribución del ingreso, entre otros– consideren también realizar mediciones sistemáticas e insesgadas de los niveles de segregación residencial socioeconómica en nuestras ciudades? Ello permitiría un genuino monitoreo de los niveles de segregación residencial, y el análisis del impacto que sobre ella tienen las políticas públicas tanto nacionales como locales, aparte de su correlación con el tamaño de las ciudades, la desigualdad socioeconómica y otros procesos sociales y políticos que operan a diferentes escalas.

Baum-Snow, N. y Pavan, R. (2013). Inequality and City Size. The Review of Economics and Statistics, 95(5), 1535-1548. https://doi.org/10.1162/REST_a_00328

Betz, D. M. (1972). The City as a System Generating Income Equality. Social Forces, 51(2), 192-198. https://doi.org/10.2307/2576336

Boustan, L. (2011). Racial Residential Segregation in American Cities. En N. Brooks, K. Donaghy y G. J. Knaap (Eds.), The Oxford Handbook of Urban Economics and Planning (pp. 318-339). https://doi.org/10.1093/oxfordhb/9780195380620.013.0015

Buzai, G. D. y Montes Galbán, E. (2021). Estadística Espacial: Fundamentos y aplicación con Sistemas de Información Geográfica. Universidad Nacional de Luján. Instituto de Investigaciones Geográficas.

Celemín, J. P. (2009). Autocorrelación espacial e indicadores locales de asociación espacial. Importancia, estructura y aplicación. Revista Universitaria de Geografía, 18, 11-31. Disponible en: http://www.redalyc.org/articulo.oa?id=383239099001

Cortese, C. F., Falk, R. F. y Cohen, J. K. (1976). Further Considerations on the Methodological Analysis of Segregation Indices. American Sociological Review, 41(4), 630-637. https://doi.org/10.2307/2094840

Cowgill, D. O. y Cowgill, M. S. (1951). An Index of Segregation Based on Block Statistics. American Sociological Review, 16(6), 825-831. https://doi.org/10.2307/2087511

Crespo, R. y Hernandez, I. (2020). On the spatially explicit Gini coefficient: the case study of Chile—a high‑income developing country. Letters in Spatial and Resource Sciences, 13, 37-47. https://doi.org/10.1007/s12076-020-00243-4

Dawkins, C. (2006). The Spatial Pattern of Black–White Segregation in US Metropolitan Areas: An Exploratory Analysis. Urban Studies, 43(11), 1943–1969. https://doi.org/10.1080/00420980600897792

Duhau, E. (2003). División social del espacio metropolitano y movilidad residencial. Papeles de Población, 9(36), 161-210. Disponible en: http://www.redalyc.org/articulo.oa?id=11203608

Duncan, O. D. y Duncan, B. (1955). A Methodological Analysis of Segregation Indexes. American Sociological Review, 20(2), 210-217. https://doi.org/10.2307/2088328

Farley, R. y Frey, W. H. (1994). Changes in the Segregation of Whites from Blacks During the 1980s: Small Steps Toward a More Integrated Society. American Sociological Review, 59(1), 23-45. https://doi.org/10.2307/2096131

Fossett, M. (2017). Aspatial and Spatial Applications of Indices of Uneven Distribution. En New Methods for Measuring and Analyzing Segregation. The Springer Series on Demographic Methods and Population Analysis (pp. 191-193). Springer Open. https://doi.org/10.1007/978-3-319-41304-4_11

Garretón, M., Basauri, A. y Valenzuela, L. (2020). Exploring the correlation between city size and residential segregation: comparing Chilean cities with spatially unbiased indexes. Environment & Urbanization, 32(2), 569-588. https://doi.org/10.1177/0956247820918983

Glaeser, E. L. y Vigdor, J. L. (2006). Racial segregation. En A. Berube, B. Katz, y R. E. Lang (Eds.) Redefining Urban and Suburban America. Evidence from Census 2000 (pp. 211-226). Brookings Institution Press.

Haque, I., Das, D. N. y Patel, P. P. (2018). Spatial Segregation in Indian Cities: Does the City Size Matter? Environment and Urbanization ASIA, 9(1), 52-68. https://doi.org/10.1177/0975425317749657

Haworth, C. T., Long, J. E. y Rasmussen, D. W. (1978). Income Distribution, City Size, and Urban Growth. Urban Studies, 15(1), 1-7. https://www.jstor.org/stable/43081466

Hwang, S.-S., Murdock, S. H., Parpia, B., y Hamm, R. R. (1985). The Effects of Race and Socioeconomic Status on Residential Segregation in Texas, 1970-80. Social Forces, 63(3), 732-747. https://doi.org/10.2307/2578489

James, D. R. y Taeuber, K. E. (1985). Measures of Segregation. Sociological Methodology, 15, 1-32. https://doi.org/10.2307/270845

Krupka, D. J. (2007). Are big cities more segregated? Neighbourhood scale and the measure of segregation. Urban Studies, 44(1), 187-197. https://doi.org/10.1080/00420980601023828

Linares, S. (2013). Medidas de segregación socioespacial: discusión metodológica y aplicación empírica sobre ciudades medias argentinas. Persona y Sociedad, 27(2), 11-40. https://doi.org/10.53689/pys.v27i2.39

Logan, J. R., Stults, B. J. y Farley, R. (2004). Segregation of minorities in the metropolis: two decades of change. Demography, 41(1), 1-22. https://doi.org/10.1353/dem.2004.0007

Long, J. E., Rasmussen, D. W. y Haworth, C. T. (1977). Income Inequality and City Size. The Review of Economics and Statistics, 59(2), 244-246. https://doi.org/10.2307/1928824

Marcos, M. y Mera, G. (2011). La dimensión espacial de las diferencias sociales. Alcances y limitaciones metodológico-conceptuales de las herramientas estadísticas para abordar la distribución espacial intraurbana. Revista Universitaria de Geografía, 20, 41-65. Disponible en: http://www.redalyc.org/articulo.oa?id=383239103002

Marcuse, P. (2001). Enclaves yes, Ghettoes no: segregation and the State. Documento presentado al “International Seminar on Segregation in the City”, Cambridge.

Massey, D. S. y Denton, N. A. (1988). The Dimensions of Residential Segregation. Social Forces, 67(2), 281-315. https://doi.org/10.2307/2579183

Morrill, R. L. (1991). On the measure of geographic segregation. Geography Research Forum, 11, 25–36. Disponible en: https://grf.bgu.ac.il/index.php/GRF/article/view/91

Nord, S. (1980). Income Inequality and City Size: An Examination of Alternative Hypotheses for Large and Small Cities. The Review of Economics and Statistics, 62(4), 502-508. https://doi.org/10.2307/1924774

Reardon, S. F. y Bischoff, K. (2011). Income Inequality and Income Segregation. American Journal of Sociology, 116(4), 1092-1153. https://www.jstor.org/stable/10.1086/657114

Reardon, S. F. y O ‘Sullivan, D. (2004). Measures of Spatial Segregation. Sociological Methodology, 34, 121-162. https://www.jstor.org/stable/3649372

Rey, S. J. y Smith, R. J. (2012). A spatial decomposition of the Gini coefficient. Letters in Spatial and Resource Sciences, 6, 55-70. http://dx.doi.org/10.1007/s12076-012-0086-z

Rodríguez, G. M. (2013). El uso de zonas censales para medir la segregación residencial: Contraindicaciones, propuesta metodológica y un estudio de caso: Argentina 1991-2001. Revista EURE - Revista De Estudios Urbano Regionales, 39(118), 97-122. http://dx.doi.org/10.4067/S0250-71612013000300005

Rodríguez, G. M. (2020). Desigualdad socioeconómica y segregación residencial en Argentina. Niveles y tendencias recientes (1991-2001-2010). Cuadernos de Vivienda y Urbanismo, 13. https://doi.org/10.11144/Javeriana.cvu13.dssr

Rodríguez Merkel, G. M. (2014). Que es y que no es segregación residencial. Contribuciones para un debate pendiente. Biblio 3W. Revista Bibliográfica de Geografía y Ciencias Sociales, 19(1079). http://www.ub.es/geocrit/b3w-1079.htm

Sabatini, F., Cáceres, G. y Cerdá, J. (2001). Segregación residencial en las principales ciudades chilenas: Tendencias de las tres últimas décadas y posibles cursos de acción. Revista EURE - Revista De Estudios Urbano Regionales, 27(82), 21-42. https://www.eure.cl/index.php/eure/article/view/1258

Shen, J. y Xiao, Y. (2020). Emerging divided cities in China: Socioeconomic segregation in Shanghai, 2000–2010. Urban Studies, 57(16), 1338-1356. https://doi.org/10.1177/0042098019834233

Taeuber, K. (1964). Negro residential segregation: trends and measurement. Social Problems, 12(1), 42-50. https://doi.org/10.2307/798696

Telles, E. E. (1995). Structural Sources of Socioeconomic Segregation in Brazilian Metropolitan Areas. The American Journal of Sociology, 100(5), 1199-1223. https://doi.org/10.1086/230636

Velázquez, G. A. (2008). Geografía y bienestar. Situación local, regional y global de la Argentina luego del Censo 2001. Editorial Universitaria de Buenos Aires.

Watson, T. (2009). Inequality and the measurement of residential segregation by income in American neighborhoods. Review of Income and Wealth, 55(3), 820-844. https://doi.org/10.1111/j.1475-4991.2009.00346.x

White, M. J. (1983). The Measurement of Spatial Segregation. The American Journal of Sociology, 88(5), 1008-1018. https://doi.org/10.1086/227768

White, M. J. (1986). Segregation and Diversity Measures in Population Distribution. Population Index, 52(2), 198-221. https://doi.org/10.2307/3644339

Winship, C. (1977). A Revaluation of Indexes of Residential Segregation. Social Forces, 55(4), 1058-1066. https://doi.org/10.2307/2577572

Wong, D. W. S. (1993). Spatial indices of segregation. Urban Studies, 30, 559–572. https://doi.org/10.1080/00420989320080551

Wong, D. W. S., Lausus, H. y Falk, R. F. (1999). Exploring the variability of segregation index D with scale and zonal systems: an analysis of thirty US cities. Environment and Planning, 31(3), 507–522. https://doi.org/10.1068/a310507

[1] En Argentina, los radios censales son las unidades espaciales más pequeñas y que tienen el mayor detalle espacial para la información censal. Mayor resolución tienen los segmentos, pero estos corresponden al área de trabajo de cada censista. En EE.UU. los estudios de segregación residencial se realizan basados en los census tracts, aunque con mayor resolución existen los census bloks utilizados para el trabajo concreto de relevamiento censal.

[2] La restricción tiene que ver con la finalidad de garantizar la confidencialidad de los informantes. Al estar agrupados en unidades espaciales suficientemente grandes, se dificulta la tarea de potenciales atacantes de reidentificar personas a través de la utilización de identificadores indirectos o criterios condicionantes.

[3] En el caso extremo, si todas las unidades espaciales contuvieran una sola vivienda, la segregación sería máxima (igual a 1); y viceversa, si todas las viviendas estuvieran agrupadas en una sola unidad (la ciudad toda) la segregación alcanzaría el mínimo posible, es decir, cero.

[4] El condado es una división político-administrativa de orden local equivalente al municipio en Argentina. Para esta escala, Krupka sólo incluyó en la muestra aquellas MSA con al menos dos condados.

[6] Tramo censal sería la traducción aproximada al castellano.

[7] Census Block en inglés, y que en realidad refiere a conjuntos de manzanas urbanas.

[8] Para este ejemplo hemos utilizado el índice de Gini, cuya definición puede consultarse en el apartado metodológico más adelante. No usamos el índice de Jargowski, pues el mismo no es compatible con variables dicotómicas.

[9] Utilizando el software ArcMap de ESRI generamos una distribución aleatoria de ambos grupos para cada nivel de agregación espacial, sólo asegurando que todas las unidades espaciales tuvieran la misma población total.

[10] En Argentina, se espera que el título primario completo se alcance a la edad de 12-13 años, mientras que el secundario completo se espera que ocurra a la edad de 17-18 años. No finalizar la educación secundaria se asume en buena medida como indicador de bajo nivel socioeconómico.

[11] El Instituto Nacional de Estadística y Censos (INDEC) aún no ha publicado los microdatos del último Censo 2022, y es improbable que esto ocurra antes de 2026-2027.

[12] Cuando se mantiene constante la superficie de la ciudad, cualquier aumento en el número de unidades espaciales (B3) o reducción en su superficie media (B4) puede interpretarse como una subdivisión de las unidades reales en más (y más pequeñas) unidades, lo que debería aumentar la segregación.

[13] Esta conceptualización alternativa del tamaño de la ciudad tiene sentido, asumiendo que probablemente estaríamos de acuerdo en que, por ejemplo, dadas dos ciudades con la misma población, la más grande es la que cubre una superficie edificada más extensa.